Scale

In the modern version of the traditional system, the master scale is organized in 12 equal tempered halfsteps (h) per octave resulting in 12ET, which gives representations of the majority of basic 3-Limit (Pythagorean) intervals in varying qualities of intonation, but does not represent basic 5-Limit, 7-Limit, 11-Limit, or 13-Limit intervals.^*

Traditional System 12h = 12ET Scale
h	0	1	2	3	4	5	6	7	8	9	10	11	12

The master scale of the Hunt system is organized in 41 commas (Ç) per octave with 5 JNDs (J) per comma resulting in 205ET, which gives excellent or perfect representations of intervals of any harmonic limit, including basic intervals of the 3-Limit, 5-Limit, 7-Limit, 11-Limit, and 13-Limit.^*

Hunt System 41Ç × 5J = 205ET Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41

A comparison of the traditional and Hunt scales requires a method of evaluation. The JND is used for this purpose, and it also functions as a basic unit of the Hunt scale. Since the JND is well defined by experimental research, we need only summarize established findings, with the goal of arriving at a tangible idea of an average sized JND to put to practical use.

* in varying qualities of intonation here refers to a range of qualities from fair to excellent, according to the Hunt IQ system of intonation evaluation, explained in the text below.

The JND

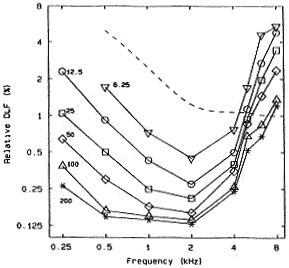
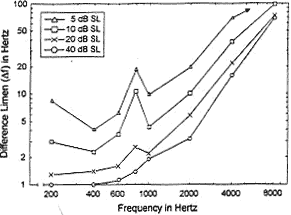
The JND for pitch referrs to differences between single successive pitches defining melodic intervals, and is also known as the Difference Limen (DL) or the Frequency Difference Limen (FDL or DLF). Although FDL is a better technical name, JND is more readily understood, so it is the term used here and elsewhere in this text. The idea of the JND relates the symbolic tone to the perceptual pitch, and although it is impossible in any one study to rigorously quantify the subjective perception of pitch in a general way, the pooling together of data from many individual studies gives a reasonable general estimation of how the abstract mathematical quantities which are tones relate to subjective perceptions which are pitches. It should also be noted that information about the JND can be found all over the internet, but a lot of it is incorrect. The JND for pitch is often said to be represented by a Weber constant of 1/333, but this has been proven false. It is also sometimes claimed that the JND is a monotonic function above 500 Hz, which also is incorrect. The Weber fraction for pitch discrimination, although not constant, does however reach the smallest of all sensory values. This means that human beings perceive changes of pitch more keenly than changes in any other sensory stimulus, such as touch, light intensity, etc. Studies on the JND use pure sine tones, and present the data in terms of Hz values and percentages, which leaves the determination of musically useful cent values to the reader. No study on this topic presents its data directly in cent values; nor do most researchers attempt to draw any musically relevant conclusions from their data. These tasks are left to musicians, presumably because the application of JND research data concerning pure sine tones may appear to be of questionable practical musical utility, since sounds which are considered "musical" generally have complex timbres corresponding to many interacting sine waves. Lacking rigorous studies, direct experience with musical application of the experimental data is currently the best evidence that such studies are musically relevant.

Average JND

An often cited early study of the JND by Shower and Biddulph (1931) found 1400 distingushable pitches between 62 and 11700 Hz, a range of about 7.5 octaves. This study suggests 1400 / 7.5 = 187 distinguishable pitches per octave, resulting in an average JND of about 6.4 cents. Subsequent research using a variety of methods has clarified these results, showing that acuity is more precise in the midrange, and is less precise at lower and higher frequencies, though not always predictably so. The pitch JND depends on many factors, and it is not a constant value. It has been shown to be a function not only of frequency but also of intensity and duration.

Moore and Glasberg (2003), Zwicker (1956, 1970), from An introduction to the Psychology of Hearing, 5th Edition, by Brian C.J. Moore, published by Academic Press, Amsterdam, Boston, 2003, p.202	Gelfand (2004) based on data of Wier et al. (1977), Hearing: an Introduction to Phychological and Physiological Acoustics, 4th Edition, Revised and Expanded, by Stanley A. Gelfand, published by Marcel Dekker, New York, 2004, p.294

The sampling of data shown above gives a relatively accurate picture of the diversity of findings concerning the JND over the years. Because of the subjective nature of pitch, as well as differences in methodology, JND values vary from one study to another, and it is often difficult if not impossible to correlate findings from different studies; however, it is clear that at this point a wide enough variety of data has been gathered in enough different ways that, given persistence in evaluating the data, the estimation of an average JND is not unreasonable. Some studies place the JND at around 30 cents below 60 Hz and even larger than this above 5 kHz (a discrimination threshold confirmed by many studies), but across the range of frequencies considered "musical" typically within these extremes, the data of many studies suggest an average JND of around 8 or 9 cents. Some studies suggest a JND as low as 3 or 4 cents between 500 Hz and 2 kHz, near where the ear is most sensitive. Based on the experimental extremes over the "musical" range, the average JND is 6 cents, as summarized in the table below.

JND	Narrow Range: 500 Hz to 2 kHz	Wide Range: 60 Hz to 5 kHz	Average
	3 to 4¢	8 to 9¢	6¢

Six cents remains the most realistic value for the average JND, confirmed over many years by many studies. There are several reference texts which summarize the experimental data in a coherent way, and the interested reader should look for the most recent text available. The data referred to here were taken from two such texts cited below the graphs shown above.

JND Measure of Intonation Quality

The average JND value can be used to create an evaluation system for the intonation quality of scale tones; that is, how well a given scale tone approximates a given target tone. The evaluation system can also be used in the context of a performance where a target pitch is known and can be compared to a pitch performed.

Hunt System of Intonation Quality (IQ)
Experimentally Confirmed JND	(none)	Narrow Range 500 Hz - 2 kHz	Average	Wide Range 60 Hz - 5 kHz	edges of musical range	outside musical range
Average JND	0	½	1	1½	2	> 2
Target	HIT				MISS
± ¢ from Target (Error)	0¢	1, 2, 3¢	4, 5, 6¢	7, 8, 9¢	10, 11, 12¢	≥ 13¢
IQ	Perfect	Excellent	Good	Fair	Poor	Wrong

This system of evaluation is called the Hunt System of Intonation Quality (IQ). The system uses a range of 0 to 9 cents intonation error within which the target pitch is said to be hit with varying qualities of intonation. At and beyond the threshold of 10 cents, the target pitch is said to be missed. The table is read as follows. If a tone is within 3 cents of the target, the intonation can be said to be excellent, because this error is within the boundary of the smallest experimentally confirmed threshold of change in pitch perception, which is also one half of the average JND. The intonation of pitches having errors of intonation up to and including the average JND of 6 cents can be called good, while those with errors greater than this and up to 9 cents (the widest experimental range of the JND and 1½ times the average JND) can be called fair. From 10 to 12 cents the intonation can be called poor, and if the error of intonation exceeds 12 cents, this being twice the average JND or larger, the intonation can be called wrong.

IQ evaluations can be given in the form of a grade, following the North American grading system A, B, C, D, F, with the addition of P for a Perfect score, and where both D and F are considered failing grades. A 12-Point scale can be used to evaluate intonation for grades P + A through D at the cent level, corresponding to an the inverse of the cents deviation, as shown in the following table.

Hunt System of IQ Grade Points
± ¢ Error	0¢	1¢	2¢	3¢	4¢	5¢	6¢	7¢	8¢	9¢	10¢	11¢	12¢	≥ 13¢
Standing	PASS										FAIL
IQ	Perfect	Excellent			Good			Fair			Poor			Wrong
Points	12	11	10	9	8	7	6	5	4	3	2	1	0	0
Grade	P	A+	A	A-	B+	B	B-	C+	C	C-	D+	D	D-	F

For evaluation purposes, errors can be rounded to the nearest cent, but cumulative errors should be calculated using all significant figures before rounding. Such a grading system allows for the expression of an Intonation Quality Grade Point Average (IQGPA) for any scale given an evaluation of any set of intervals. Below, this system of evaluation is used to outline and compare the traditional scale and the Hunt scale.

Traditional System

Although this text is not primarily an historical investigation, it is still helpful to view the modern version of the traditional chromatic scale in the context of the long and circuitous path of Western music history. Only Stage 1 and Stage 4 shown below have so far been investigated in the chapters of this text; the other stages may form the basis of future chapters which, when completed, will preceed the present discussion.

Historical Stage	1	2	3	4
Approximate Years	500 B.C.E. - 1500 C.E.	1500-1750	1650-1800	1750-present
Tuning Name	Pythagorean	Meantone Tempered	Well Tempered	Equal Tempered
Harmonic Limits	Pure 3-Limit	Mistuned 3-Limit Nearly Pure 5-Limit	Mixed Quality 3- and 5-Limit	Mistuned 3-Limit
IQ, Fifths 2:3:4 Thirds 4:5:6	Perfect Fifths Wrong Thirds*	Good Fifths 1 Wrong Fifth Excellent Thirds	Mixture of Perfect, Excellent, Good and Fair Fifths and Thirds	Excellent Fifths Wrong Thirds
Step Sizes	Unequal			Equal
Shape of 3-Limit Cycle	Spiral		Circle
Number of Tones	7-13	12-31	12

Thanks to Claudio di Veroli, historical tunings scholar and author of Unequal Temperaments, for corrections concerning the Approximate Years.

* Calling 5-Limit thirds "Wrong" in a 3-Limit system might seem to beg the question, aren't 3-Limit thirds the "Perfect" thirds for that system? Yes, the thirds 27:32 and 64:81 would of course both be intoned as "Perfect" in a 3-Limit system, which emphasizes that what is being called "Wrong" is the intonation (IQ see above) of a specific pair intervals, in this case 4:5 and 5:6 as judged within each system.

Whether or not the Western scale as such can be characterized as an entity before around 1500 is debatable, but for our purposes we will be content to observe its origins as a pure 3-Limit diatonic system which expanded into a 13-tone spiral of fifths. Note that the historical periods given here overlap, and are only approximate. From 1500 onwards, the Western scale was altered from its 3-Limit form and sometimes massively expanded to incorporate basic 5-Limit intervals, reaching as many as 31 tones to allow for greater flexibilty of pitch center on an expanded spiral of fifths. Within a century the scale was further transformed through a plethora of temperaments which deliberately mistuned either or both the 3-Limit and 5-Limit intervals in an effort to close the spiral and make all pitch centers useable and unique. Finally, returning home as it were, some 300 years later the scale was returned to a mistuned but tolerable version of the original 3-Limit system, known as 12ET, where the spiral is turned into a circle, all pitch centers are useable but sound equally out of tune, and all steps in the scale are equal in size. A more direct path to this system is outlined in Chapter 3. 12ET and its relationship to its historical origin is summarized in the figures below.

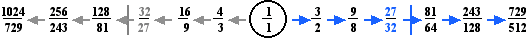
It is the close proximity of the 3-Limit gamut to the equal division of 12 which makes the unit of the cent a reasonable choice for measuring musical intervals. The small distances each interval strays from the 100¢ tick marks in the figure above are simply thrown out in the 12ET version of the traditional system. So, one could say that the deep structure remains, while the surface detail is lost.

Traditional System 12h = 12ET Scale
h	0	1	2	3	4	5	6	7	8	9	10	11	12

Considering how a scale functions in terms of expressing pitches and intervals, each scale step can be viewed as the center of a categorical tuning zone within which a number of pitches and intervals may fall. Each step of 12ET functions is a zone of ±50¢. Below are shown the first four steps of the 12ET scale, as cents tuning zones in the right table.

12ET Scale Steps h 0 1 2 3	→	12ET Tuning Zones ±50¢ 0¢ .. 50¢ 50¢ .. 150¢ 150¢ .. 250¢ 250¢ .. 350¢ h Zone 0¢ 100¢ 200¢ 300¢

Each value in the cells marked h Zone in the bottom row of the right table gives the center of a step zone, the range of which is given in the field directly above it. For example, step 3 or 12ET has a center tuning of 300¢, and is used to represent all intervals between 250¢ and 350¢. It is easily seen that 12ET guarantees a maximum target tuning error of ±50¢. Comparing this to the range of tuning errors considered acceptible according to the IQ system, the 12ET scale passes for only 18% of all possible pitches.

12ET Scale IQ
Target	18% PASS										82% FAIL
± ¢ Error	0¢	1¢	2¢	3¢	4¢	5¢	6¢	7¢	8¢	9¢	10¢	11¢	12¢	13¢	14¢	15¢	16¢	17¢	18¢	19¢	20¢	21¢	22¢	23¢	24¢	25¢	26¢	27¢	28¢	29¢	30¢	31¢	32¢	33¢	34¢	35¢	36¢	37¢	38¢	39¢	40¢	41¢	42¢	43¢	44¢	45¢	46¢	47¢	48¢	49¢	50¢
IQ	Perfect	Excellent			Good			Fair			Poor			Wrong
Points	12	11	10	9	8	7	6	5	4	3	2	1	0	0
Grade	P	A+	A	A-	B+	B	B-	C+	C	C-	D+	D	D-	F

Of course, the small percentage of pitches which are acceptibly represented by 12ET form the core of the 3-Limit system. Below, the 13-Limit gamut is compared to the tones of the 12ET scale, with IQ grades given in the last row, averaged below the table.

13-tone Pythagorean Gamut
Ratio	1 1	256 243	9 8	32 27	81 64	4 3	1024 729	729 512	3 2	128 81	27 16	16 9	243 128	2 1
¢	0¢	90.2¢	203.9¢	294.1¢	407.8¢	498¢	588.3¢	611.7¢	702¢	792.2¢	905.9¢	996.1¢	1109.8¢	1200¢
Traditional 12ET Chromatic Scale
h	0	1	2	3	4	5	6		7	8	9	10	11	12
¢	0¢	100¢	200¢	300¢	400¢	500¢	600¢		700¢	800¢	900¢	1000¢	1100¢	1200¢
±¢	±0¢	+9.8¢	-3.9¢	+5.9¢	-7.8¢	+2¢	±11.7¢		-2¢	+7.8¢	-5.9¢	+3.9¢	-9.8¢	±0¢
IQ		Poor D+	Good B+	Good B-	Fair C	Excellent A	Poor D-		Excellent A	Fair C	Good B-	Good B+	Poor D+

Not surprisingly, 12ET scores well for 3-Limit intervals; however, this is not the case for basic intervals of the 5-Limit.

13 Basic 5-Limit Intervals
Ratio	1 1	16 15	10 9	6 5	5 4	27 20	45 32	64 45	40 27	8 5	5 3	9 5	15 8	2 1
¢	0¢	111.7¢	182.4¢	315.6¢	386.3¢	519.6¢	590.2¢	609.8¢	680.4¢	813.7¢	884.4¢	1017.6¢	1088.3¢	1200¢
Traditional 12ET Chromatic Scale
h	0	1	2	3	4	5	6		7	8	9	10	11	12
¢	0¢	100¢	200¢	300¢	400¢	500¢	600¢		700¢	800¢	900¢	1000¢	1100¢	1200¢
±¢	±0¢	-11.7¢	+17.6¢	-15.6¢	+13.7¢	-19.6¢	±9.8¢		+19.6¢	-13.7¢	+15.6¢	-17.6¢	+11.7¢	±0¢
IQ		Poor D-	Wrong F	Wrong F	Wrong F	Wrong F	Poor D+		Wrong F	Wrong F	Wrong F	Wrong F	Poor D-

According to the IQ system, 12ET similarly fails to represent intervals of the 7-Limit, 11-Limit, and 13-Limit. 12ET incidentally does have good representations of some basic 17-Limit and 19-Limit intervals, but lacking basic intervals from lower limits gives these higher prime limit intervals inadequate context within which to function according to their harmonic identities. Historically speaking, many other systems have been suggested to remedy the defects of 12ET, some of which are discussed in Chapter 6; however, such previously suggested systems have not been complete in their harmonic flexibility, have not been manageable in terms of the number of tones required, and have not been thoroughly developed in terms of the nomenclature, notation, and instruments required to use them. Having established these defects, we turn our attention to a system designed in such a way that all all of these issues are addressed.

Hunt System

The Hunt system represents a synthesis of traditional Western music theory and modern psychoacoustic research. It is based on the premise that average limits of human pitch perception should determine the measure of pitch, and this measure should expand and clarify the traditional structures of Western music. The master scale of the system makes practical use of average units of measure, both theoretical and perceptual. It is constructed from two basic units, the ancient theoretical unit of the comma and the modern perceptual unit of the just noticeable difference (JND), so that the octave is divided equally by both units. The system resolves the basic problems dealt with in different ways by the previous historic stages of the history of the Western musical scale.

Hunt System Master Scale
Tuning Name	Harmonic Limits	IQ, Fifths 2:3:4 Thirds 4:5:6	Shape of 3-Limit Cycle	Number of Tones
JND Scale Perceptual Scale Average Units Scale Hunt Scale 205ET	Unlimited	Perfect Fifths Perfect Thirds All Others: Excellent or Perfect	Circle	41Ç × 5J = 205

The average sized JND has been established. Below, the rationale for the establishment of an average sized comma is given.

The Comma

The comma bears some relationship with the JND, as it also deals with differences in pitch on the order of a few JNDs, but it is primarily theoretical rather than experimental. The comma is one of the most important theoretical ideas in Western music history, although it is not normally discussed with much detail in modern Western music education. As is the case elsewhere in this text, the following discussion is empirical rather than historical, though historical information is given when it is both relevant and logical. As with the JND, our goal is to arrive at a tangible idea of an average sized comma which can be put to practical systematic use in terms of a musical scale.

Commas are intervals which are quite a bit smaller than the halfsteps of 12ET, but typically larger than JNDs. A useful way to think of a comma is as a "near miss", either mathematically or perceptually. From a mathematical point of view, the difference between two tones which are very nearly but are not the same value defines a comma. From a perceptual point of view, a comma is the perceived distance between two pitches that are heard as different but are close enough to be considered in the same category. According to the perceptual definition, a comma would have to be at least as large as a single JND, but the comma is primarily a theoretical construct, and some commas are in fact smaller than a single JND. One useful rule of thumb is that the size of a comma does not exceed a quartertone (50¢) of 12ET. The most famous comma in Western music history is the Pythagorean Comma, which was an arrival point at the end of Chapter 3, summarized below.

Historical Name	Colloquial Name	Difference Between Tones	Interval	Size in Cents
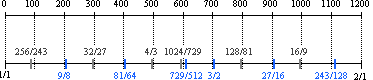
Pythagorean Comma	Fifths Comma, Comma	729/512 and 1024/729	524288:531411	23.36228¢

The Pythagorean comma involves only powers of the prime numbers 2 and 3, and it results from a symmetrical cyclic structure created from successive powers of 3. The second most notable comma involves the next higher prime: 5, discussed in Chapter 5 and summarized below.

Historical Name	Colloquial Name	Difference Between Tones	Interval	Size in Cents
Syntonic Comma, Comma of Didymus, Comma of Ptolomy	Thirds Comma, Comma	5/4 and 81/64	80:81	21.50629¢

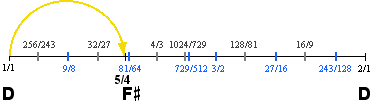
The difference between these two commas is so small (1.85599¢, another comma known as the skisma) that both commas have been considered perceptually equivalent throughout history, such that whenever the term comma is used without further clarification, it is assumed to refer to either or both of the above intervals; but, these are not the only commas of interest. While not as pervasive as either of the above commas, another basic historical comma is derived from the prime number 7, introduced in summary below.

Historical Name	Colloquial Name	Difference Between Tones	Interval	Size in Cents
Comma of Archytas	Sevenths Comma, Septimal Comma	7/4 and 16/9	63:64	27.26409¢

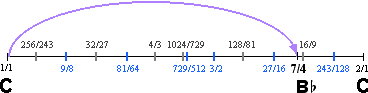
Some useful observations can be made concerning these three important historical commas. First, notice that the Fiths Comma is derived from a symmetrical cycle of powers of the prime number 3, while the Thirds Comma and Sevenths Comma are defined not by cycles of 5 and 7, but by deviations of the basic harmonic intervals 5/4 and 7/4 from the 3-Limit structure. Notice also that only the Fifths Comma can be represented directly in traditional notation (G to A), with a traditional interval name (the diminished second d2), while there is no standard way to specify either the Thirds Comma or Sevenths Comma in traditional notation or interval terminology. These important distinctions suggest two categorical types of commas: the cyclic or n-Cycle Comma and the harmonic or n-Comma, where n is the highest prime number involved. Although there is no historical precedent for such a distinction, this way of thinking leads towards our goal of establishing an average sized comma. Each concept is explored in turn below.

n-Commas

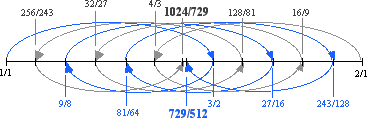
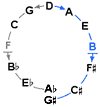
Dispensing with historical and colloquial names in favor of systematic logic, we categorically separate the 3-Cycle Comma from the harmonic commas. A harmonic or n-Comma may be classified by its proximity to a given tone of the 3-Limit, or around what 3-Limit degree the comma is found. For this purpose, it is helpful to refer to each of the tones of the 3-Limit gamut by name, as derived in Chapter 3, summarized in the figure below.

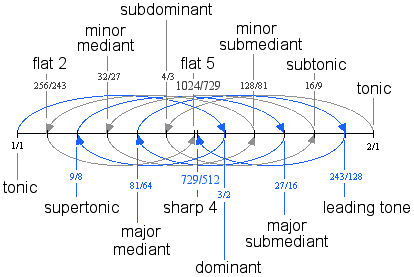
To find an n-Comma, the nth-harmonic is compared to all the tones of the 3-Limit gamut, looking for the nearest match, or smallest difference. The results for the primes 5 through 17 are shown below.

Systematic Name	Found around Degree	Difference Between Tones	Interval	Size in Cents
5-Comma	major mediant	5/4 and 81/64	80:81	21.50629¢
7-Comma	subtonic	7/4 and 16/9	63:64	27.26409¢
11-Comma	flat 5	11/8 and 1024/729	8019:8192	36.95205¢
13-Comma	minor submediant	13/8 and 128/81	1024:1053	48.34767¢
17-Comma	flat 2	17/16 and 256/243	4096:4131	14.73041¢

Considering the n-commas from 5 through 17 as a group, the average comma size is 29.7601¢. Although this set of harmonic intervals represents a reasonable perceptual gamut, it is far from an exhaustive list. If we continue this process for higher primes until we have accounted for at least one deviation for every tone in the 13 tone gamut, we reach the 53-Limit.

Systematic Name	Found around Degree	Difference Between Tones	Interval	Size in Cents
19-Comma	minor mediant	19/16 and 32/27	512:513	3.378019¢
23-Comma	sharp 4	23/16 and 729/512	729:736	16.54434¢
29-Comma	subtonic	29/16 and 16/9	256:261	33.4872¢
31-Comma	leading tone	31/16 and 243/128	243:248	35.26057¢
37-Comma	minor mediant	37/32 and 32/27	999:1024	42.79096¢
41-Comma	major mediant	41/32 and 81/64	81:82	21.2424¢
43-Comma	subdominant	43/32 and 4/3	128:129	13.47271¢
47-Comma	dominant	47/32 and 3/2	47:48	36.44838¢
53-Comma	submediant	53/32 and 27/16	53:54	32.36046¢

Considering the n-commas from 5 through 53 as a group, the average comma size is 27.59367¢. The relevance of averaging in commas above the 53-Limit is debatable, considering that even above the 23-Limit, the primary harmonic intervals become increasingly weak in terms of perceptual clarity. Even so, for the sake of transparency, we can extend the limit further. Primes within the 96-Limit end with the 89th harmonic, as shown below.

Systematic Name	Found around Degree	Difference Between Tones	Interval	Size in Cents
59-Comma	leading tone	59/32 and 243/128	236:243	50.60335¢
61-Comma	leading tone	61/32 and 243/128	243:244	7.109801¢
67-Comma	flat 2	67/64 and 256/243	67:72	10.91797¢
71-Comma	supertonic	71/64 and 9/8	71:72	24.21346¢
73-Comma	supertonic	73/64 and 9/8	72:73	23.87947¢
79-Comma	major mediant	79/64 and 81/64	79:81	43.28311¢
83-Comma	major mediant	83/64 and 81/64	81:83	42.22731¢
89-Comma	flat 5	89/64 and 1024/729	64881:65536	17.38988¢

Considering the n-commas from 5 through 89 as a group, the average comma size is 27.42772¢. There is so little difference between the 5-53 and 5-89 averages that we have little reason to continue the process, especially considering that doing so would lead to a predictable and not very meaningful resulting average comma size equal to the mean difference between all of the tones in the 3-Limit gamut. The data so far are much more meaningful, showing clearly that the average size of n-commas moves from near 30¢ for lower harmonics to around 27¢ for higher harmonics.

The data for the set of n-commas from the 5- to 89-Limit gives an average sized n-comma of 27.4¢.

n-Cycle Commas

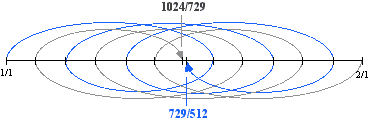
An n-cycle comma is fundamentally different from an n-comma. The n-cycle comma may be categorized mathematically by the power to which a prime is raised to arrive at an interval which when compared to its inversion defines a comma. For example, the 3-Cycle comma occurs at the 6th power of 3 (3^6 = 729), as shown below.

By beginning at an endpoint on the number line above and following the curve of the gray or blue line as it travels above and below the number line, it can be seen that the number of arcs is equal to the number of powers to which 3 has been raised. For each line, gray or blue, there are six arcs, leading to (blue line) harmonic 729/512 and (gray line) subharmonic 1024/729, defining the 3-Cycle comma.

n-Cycle	Power	Size in Cents
3	^6	23.36228¢

All n-cycle commas converge around the center of the octave, with varying gap widths and varying numbers of arcs (powers) needed to arrive at the central near miss. The next n-cycle comma after the 3-Cycle is the 5-Cycle.

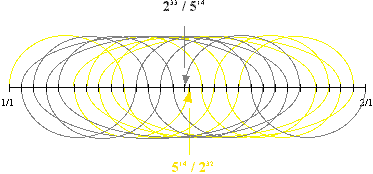
For each line, gray or yellow, there are fourteen arcs, leading to (yellow line) harmonic 5¹⁴/2³² and (gray line) subharmonic 2³³/5¹⁴, defining the 5-Cycle comma. Because the numbers are so large, and the only important aspect of the numbers for our purposes is the power to which each prime is raised, the ratios are shown as powers of primes.

n-Cycle	Power	Size in Cents
5	^14	16.78399¢

The next n-cycle comma after the 5-Cycle is the 7-Cycle.

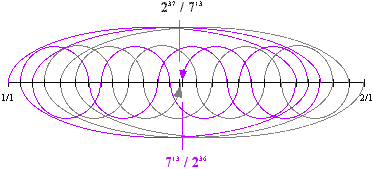
For each line, gray or violet, there are thirteen arcs, leading to (violet line) harmonic 7¹³/2³⁶ and (gray line) subharmonic 2³⁷/7¹³, defining the 7-Cycle comma.

n-Cycle	Power	Size in Cents
7	^13	10.52643¢

Many n-cycle commas require high powers, so that graphing them becomes quite messy. For this reason we dispense with showing additional n-cycle commas graphically, considering the concept understood well enough to imagine how the results might look on a tone ruler. We will use the same range of harmonics for n-cycle commas as for n-commas, stopping at the primes below 96. This means considering n-cycle commas for the prime harmonics 3 through 89, as shown in the continuation of the table below.

n-Cycle Power Size in Cents 11 ^12 31.63062¢ 13 ^5 5.276618¢ 17 ^17 31.51608¢ 19 ^2 9.947935¢ 23 ^22 44.07128¢ 29 ^67 36.65598¢ 31 ^11 9.217406¢ 37 ^12 32.25693¢ 41 ^7 6.873678¢ 43 ^27 21.9561¢	n-Cycle Power Size in Cents 47 ^37 47.49003¢ 53 ^46 37.58182¢ 59 ^30 49.70045¢ 61 ^7 36.38727¢ 67 ^23 48.12331¢ 71 ^10 6.069132¢ 73 ^8 44.63153¢ 79 ^5 45.36898¢ 83 ^4 0.3785409¢ 89 ^20 35.20469¢

Considering the n-cycle commas from 3 through 89 as a group, the average comma size is 27.43526¢. It should be noted that extending this limit further slightly increases the average size. Considering all the primes from 3 through 1021, the average n-cycle comma becomes 28.72166¢. We will use the smaller subset, so that this data parallels that of the n-comma, and as will be seen in the concluding section, using the higher value would only help our argument.

The data for the set of n-cycle commas from the 3- to 89-Limit gives an average sized n-comma of 27.4¢.

Average Comma

Both the n-commas and the n-cycle commas averaged over the range of all the prime harmonics between 3 and 96 give an empirically derived value of 27.4¢ for an average comma. Note that the n-comma by definition does not include the 3-Limit, as all n-commas are calculated relative to the 3-Limit 13 tone gamut. Note also that this value is almost exactly the size of the historical Comma of Archytas, the septimal comma of 27.3¢.

Comma Type	Harmonics	Average Size
n-comma	4:5 through 64:89	27.42772¢
n-cycle	2:3 through 64:89	27.43526¢
Average Comma		27.43149¢
Comma of Archytas	63:64	27.3¢

Although the idea of the average comma is derived here as a theoretical rather than psychophysical unit of measure, the results can be interpreted as defining the average limits of categorical pitch naming. In other words, according to the theory outlined here, pitches falling within the range of 27.4¢ of each other should be considered in the same category (two kinds of C, for example), whereas pitches further apart than this should tend to sound as if they belong to different pitch categories. This idea of boundaries and sameness of category has important implications for the use of the average comma within a musical scale, as discussed below.

Master Scale

Having determined both the average JND and the average comma, the following question arises. How many average JNDs are there in an average comma? The following relationship is found.

	Average Size ¢	J/Ç
J	6¢	21.87%
Ç	27.43149¢

The average JND is about 1/5 (20%) the size of an average comma.

For maximal flexibility, the Hunt system maintains the modern principle of an equal division of an octave as its master scale, but instead of limiting this division to the 12ET halfstep, the equal units are directly related to the average comma and JND, keeping in mind the near 20% relationship between the two values. The table below shows an intitial comparison of these values to equal divisions of an octave.

	Average Size ¢	Closest ET	ET Step Size	J/Ç	Difference ¢
J	6¢	200ET	6¢	20.27%	0¢
Ç	27.43149¢	43ET	27.9¢		0.5¢

When the 43ET step is used as the average comma, we see that the J/Ç ratio more closely approaches 20%. Recall that 43ET is derived from the the 43-Tone 3-Limit cycle, explored in detail in Chapter 6, summarized below.

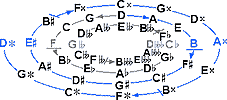
The 43-tone 3-Limit cyclic system introduces triple accidentals, and at the edges of the system altered versions of the tonic are found, D and D, which spell a sextupally diminished octave sounding almost as a perfect fourth — a fact of immense significance, because historically it was the lack of a perfect fourth between the end tones of the diatonic naturals that brought about the use of accidentals in the first place. So it should be emphasized that the 43-tone 3-Limit cycle systemically resolves one of the most fundamental problems in Western music, namely tritone correction.

When all of the steps of this system are made the same size, the result is 43ET, a scale with fairly good thirds but rather flat fifths, such that it cannot be considered an improvement over 12ET. However, the alternate method of handling the 43-tone 3-Limit cycle gives 41ET, which has nearly pure fifths and good thirds, both better than 12ET.

Average Comma	Chosen ET	ET Step Size	Difference ¢
27.43149¢	41ET	29.26829¢	+1.83680¢

The difference between the average comma and the 41ET step should look familiar, as it is almost exactly the same as the skizma of 1.85599¢, an interval so small that pitches differing by this amount have historically been considered identical. Modern research confirms that the skizma, 1/3 average JND in size, is an interval which practically speaking can simply be ignored. Further, because the empirically derived average comma defines an interval within which pitches should be considered categorically similar, it also stands to reason that the interval used to create a scale based on the average comma should ideally consist of steps which are just a bit wider than the average comma, so that successive steps of the scale can clearly represent distinct pitches. 41ET is exactly this scale. Using the 41ET step as the average comma, the average JND can be taken as 1/5 (20%) of each step. This results in 205ET, as shown below.

Average JND	Chosen ET	ET Step Size	Difference ¢
6¢	41 × 5 = 205ET	5.85366¢	-0.146¢

Whereas the experimental value of the average comma as a theoretical unit suggested a slightly larger value for use in a scale, outside the exprimental boundary so that pitches will be clearly defined by category, the average experimental JND value as a psychophysical unit suggests a slightly smaller value be used in a musical scale, inside the experimental boundary so that the noticeable difference is made more subtle. The ideal values for the average comma and JND are very slightly adjusted from the experimental values. These differences and the advantages gained from adopting the adjusted values for use in a musical scale are shown in the table below.

	Average Size ¢	J/Ç	Chosen ET	ET Step Size	J/Ç	Difference ¢	Comments
J	6¢	21.87%	205ET	5.85¢	20%	-0.146¢	Slightly smaller J ensures less noticeable error (better tuning precision)
Ç	27.43149¢		41ET	29.26829¢		+1.83680¢	Slightly larger Ç ensures more distinct scale steps (better categorical pitch)

Further, a direct relationship of exactly 20% (1/5) between Ç and the J allows Ç to function as a categorical scale step and for J to function as a fine tuning inflection within each step. Each 41ET Ç step can be seen as a coarse tuning step zone of ±14.6¢, and each 205ET J inflection as a fine tuning inflection zone of ±2.9¢. Below are shown the first four steps of the master scale, as steps and inflections in the left table and as cents tuning zones in the right table.

Steps and Inflections 205ET Inflection +2J +1J ±½ J -1J -2J 2 1 0     7 6 5 4 3 12 11 10 9 8 17 16 15 14 13 41ET Step Ç 0 1 2 3	→	Tuning Zones Inflection Zone +2J +1J ±½ J -1J -2J 8.8¢ .. 14.6¢ 2.9¢ .. 8.8¢ -2.9¢ .. +2.9¢     38¢ .. 43.9¢ 32.2¢ .. 38¢ 26.3¢ .. 32.2 20.5¢ .. 26.3¢ 14.6¢ .. 20.5¢ 73.2¢ .. 79¢ 67.3¢ .. 73.2¢ 61.5¢ .. 67.3¢ 55.6¢ .. 61.5¢ 43.9¢ .. 55.6¢ 102.4¢ .. 108.3¢ 96.6¢ .. 102.4¢ 90.7¢ .. 96.6¢ 84.9¢ .. 90.7¢ 79¢ .. 84.9¢ Step Zone Ç 0¢ 29.3¢ 58.5¢ 87.8¢

Each value in the cells marked Step Zone in the bottom row of the right table gives the center of a step zone, the full range of which is given in the large field of inflection zones directly above it. Note that each inflection zone spans ±½J, so for example the range for rows marked +1J in fact range from +½ J to +1½ J. Similarly, each step zone spans a range of ±½ Ç, or ±14.6¢. The central range of the inflection zone is underlined, showing that the center of this range is the center of the step. A complete table of steps and inflections is shown below.

Hunt System 41Ç × 5J = 205ET Scale
Inflection	+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Step	Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41

The use of inflections guarantees a maximum target fine tuning error of ½ J = 2.93¢, resulting in either perfect or excellent intonation of all pitches according to the IQ system.

Hunt System Master Scale IQ
Target	100% HIT
± Error¢	0¢	1¢	2¢	3¢
J ±¢	0 J ±0¢	½ J ±2.9¢
IQ	Perfect	Excellent
Points	12	11	10	9
Grade	P	A+	A	A-

The worst IQGPA possible in the Hunt system is 9, A- (Excellent), as shown below in several tables mapping basic intervals^* of the 3-Limit, 5-Limit, 7-Limit, 11-Limit, and 13-Limit onto the master scale, with IQ values given at the bottom row and summarized below each table.

* A basic interval involves only the prime of a limit and the primes 2 and 3. For example, 4:7 is a basic interval, but 5:7 is not. Systematic classifications of harmonic ratio intervals is the topic of a chapter which is not yet included here.

13-Tone Pythagorean Gamut
Ratio	1 1			256 243				9 8			32 27				81 64			4 3			729 512	1024 729			3 2			128 81				27 16			16 9				243 128			2 1
¢	0¢			90.2¢				203.9¢			294.1¢				407.8¢			498¢			588.3¢	611.7¢			702¢			792.2¢				905.9¢			996.1¢				1109.8¢			1200¢
Hunt 205ET JND Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41
¢	0¢			87.8¢				204.9¢			292.7¢				409.8¢			497.6¢			585.4¢	614.6¢			702.4¢			790.2¢				907.3¢			995.1¢				1112.2¢			1200¢
±¢	±0¢			-2.4¢				+1¢			-1.4¢				+2¢			-0.4¢			-2.9¢	+2.9¢			+0.4¢			-2¢				+1.4¢			-1¢				+2.4¢			±0¢
IQ	P			A				A+			A+				A			P			A-	A-			P			A				A+			A+				A			P

14 Basic 5-Limit Intervals
Ratio	1 1	81 80			16 15		10 9					6 5		5 4					27 20		45 32	64 45		40 27					8 5		5 3					9 5		15 8			160 81	2 1
¢	0¢	21.5¢			111.7¢		182.4¢					315.6¢		386.3¢					519.6¢		590.2¢	609.8¢		680.4¢					813.7¢		884.4¢					1017.6¢		1088.3¢			1178.5¢	1200¢
Hunt 205ET JND Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41
¢	0¢	23.4¢			111.2¢		181.5¢					316.1¢		386.3¢					521¢		591.2¢	608.8¢		679¢					813.7¢		883.9¢					1018.5¢		1088.8¢			1176.6¢	1200¢
±¢	±0¢	+1.9¢			-0.5¢		-0.9¢					+0.5¢		±0¢					+1.4¢		+1¢	-1¢		-1.4¢					±0¢		-0.5¢					+0.9¢		+0.5¢			-1.9¢	±0¢
IQ	P	A			P		A+					P		P					A		A+	A+		A					P		P					A+		P			A	P

12 Basic 7-Limit Intervals
Ratio	1 1	64 63	28 27						8 7	7 6						9 7	21 16									32 21	14 9						12 7	7 4						27 14	63 32	2 1
¢	0¢	27.3¢	63¢						231.2¢	266.9¢						435.1¢	470.8¢									729.2¢	764.9¢						933.1¢	968.8¢						1137¢	1172.7¢	1200¢
Hunt 205ET JND Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41
¢	0¢	29.3¢	64.4¢						228.3¢	269.3¢						433.2¢	468.3¢									731.7¢	766.8¢						930.7¢	971.7¢						1135.6¢	1170.7¢	1200¢
±¢	±0¢	+2¢	+1.4¢						-2.9¢	+2.4¢						-1.9¢	-2.5¢									+2.5¢	+1.9¢						-2.4¢	+2.9¢						-1.4¢	-2¢	±0¢
IQ	P	A	A+						A-	A						A	A-									A-	A						A	A-						A+	A	P

6 Basic 11-Limit Intervals
Ratio	1 1					12 11							11 9							11 8			16 11							18 11							11 6					2 1
¢	0¢					150.6¢							347.4¢							551.3¢			648.7¢							852.6¢							1049.4¢					1200¢
Hunt 205ET JND Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41
¢	0¢					152.2¢							345.4¢							550.2¢			649.8¢							854.6¢							1047.8¢					1200¢
±¢	±0¢					+1.6¢							-2¢							-1.1¢			+1.1¢							+2¢							-1.6¢					±0¢
IQ	P					A							A							A+			A+							A							A					P
6 Basic 13-Limit Intervals
Ratio	1 1					13 12							16 13							18 13			13 9							13 8							24 13					2 1
¢	0¢					138.6¢							359.5¢							563.4¢			636.6¢							840.5¢							1061.4¢					1200¢
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41
¢	0¢					140.5¢							357.1¢							562¢			638¢							842.9¢							1059.5¢					1200¢
±¢	±0¢					+1.9¢							-2.4¢							-1.4¢			+1.4¢							+2.4¢							-1.9¢					±0¢
IQ	P					A							A							A+			A+							A							A					P

The basic harmonic intervals from the 3-Limit through the 13-Limit combine to give unique representations for each comma zone of 41ET, requiring only single JND deviations from the central chain of fifths in 41ET. Investigations of pitch and interval naming clarify the logic and usefulness of this structure, showing that it is clearly no accident.

Hunt System 41Ç × 5J = 205ET Scale
+2J +1J ±½ J -1J -2J	2 1 0	7 6 5 4 3	12 11 10 9 8	17 16 15 14 13	22 21 20 19 18	27 26 25 24 23	32 31 30 29 28	37 36 35 34 33	42 41 40 39 38	47 46 45 44 43	52 51 50 49 48	57 56 55 54 53	62 61 60 59 58	67 66 65 64 63	72 71 70 69 68	77 76 75 74 73	82 81 80 79 78	87 86 85 84 83	92 91 90 89 88	97 96 95 94 93	102 101 100 99 98	107 106 105 104 103	112 111 110 109 108	117 116 115 114 113	122 121 120 119 118	127 126 125 124 123	132 131 130 129 128	137 136 135 134 133	142 141 140 139 138	147 146 145 144 143	152 151 150 149 148	157 156 155 154 153	162 161 160 159 158	167 166 165 164 163	172 171 170 169 168	177 176 175 174 173	182 181 180 179 178	187 186 185 184 183	192 191 190 189 188	197 196 195 194 193	202 201 200 199 198	205 204 203
Ç	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41

NEXT: Pitches