In this chapter, the system is extended to the 5-limit and basic structures called triads are derived.
We began our exploration of the Western system by systematically dividing a viola string into vibrating segments. The first four subdivisions of the string contain only one new tone: the third harmonic. These tones are reviewed below.
Working within this 3-limit has allowed us to build the 13 tone system, yet the harmonic series does not end at 4. Further exploration yields important discoveries.
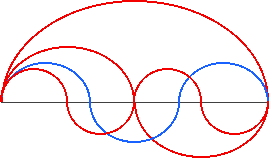
We continue counting where we left off previously, to reach the second odd prime number 5. If the string is touched and bowed at a point one fifth of the way along the neck of the viola, a second new pitch is produced.
This is the fifth harmonic in the harmonic series. The five arcs below show that the string is broken into fifths.
The vibrating segment is one fifth as long as the whole string, so we can call this segment 1/5. This segment also vibrates 5 times as fast as the first tone. The figure above is shown in yellow to signify that the number 5 represents the second new tone. The value of this tone, 5, is obviously larger than 2. To justify this tone, we use the relationship of duplication, dividing the tone by 2 twice, which gives us 5/2, and then 5/4, congruences of 5 which sound increasingly lower in pitch.
Having justified the second new tone, we can see how it fits within the boundary tones.
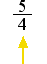
As the second new tone, 5/4 has a prominant function in the structure of the Western system. What should this new tone be called?.
Consider the 13 tones derived within the 3-limit.
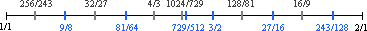
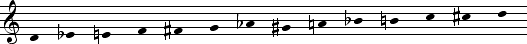
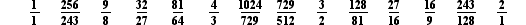
Our inventory of tones includes seven naturals, three sharps and three flats. The names of these 13 tones serve as standards from which new labels may be derived.
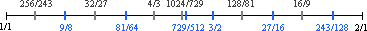
The tone 5/4 is close to the Major Mediant 81/64, F
.
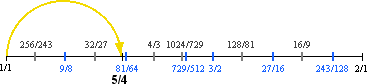
Because the new tone results from the fifth harmonic and falls near the Pythagorean major mediant, it is called the harmonic mediant.
F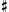 is used to label the new tone, but it
obviously does not sound the same as its Pythagorean neighbor. The small interval between
these two tones is similar to the small interval known as the Pythagorean Comma at
the middle of the 13 tone system. This new comma, located around the third diatonic
scale degree, is known as the Syntonic Comma or Thirds Comma.
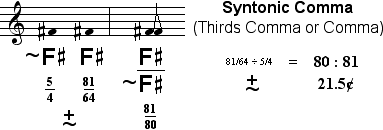
The symbol used here to represent the Syntonic Comma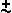 
is the same as the symbol used previously to represent the Pythagorean comma
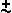. It is a combination of two symbols called
shifts: a negative shift 
and a
positive shift 
. When tones separated by commas
share the same letter and accidental, a shift can be used to label the
non-Pythagorean tone. The tilde is used when
the new tone is lower than its Pythagorean neighbor. The prefix sub
is standard in music theory to mean that which is below. Therefore, the shift
indicating the lower tone can be called a sub shift, so that
F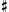 is called sub F sharp.
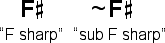
This terminology can be used to distinguish a tone which is lower from a Pythagorean
tone by a comma, in this case the Syntonic Comma. The figure below shows the correct
derivation of both varieties of F.
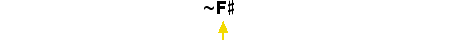
The new tone results in a new type of Major Third. What should this new interval be called? Just as the name of the new tone was taken from the Pythagorean tone 81/64, the Pythagorean interval 64:81 should also maintain the standard name Major Third, or M3. The slightly smaller comma shifted Major Third may thus be called the Small Major Third, or SM3. This smaller third can also be called the Just Major Third.
Next we see how the Small Major Third functions as a preferred harmonic interval.
NEXT: Major Triad