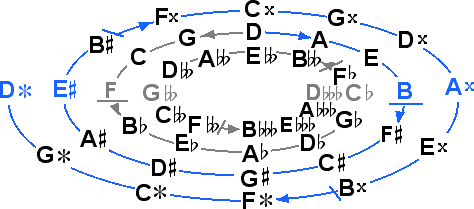
The 43 tone system contains huge ratios having up to eleven digits, and includes new triple accidentals that correspond to adjacent scale steps that are a fifth apart in terms of raw staff distance, as shown below.
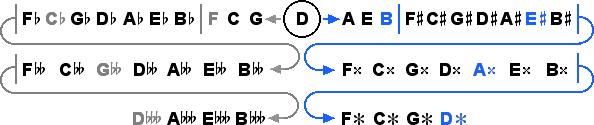
The egdes of this system give us a very curious interval indeed; a sextupally diminished octave, between
D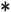
and D
.
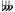The fact that these tones are altered versions of the tonic suggests that this system
has some special significance.
The end tones are color coded below to show their relationships with the end tones F and B of the
diatonic naturals (as well as G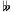
and
A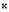
of the 31 tone system, and E
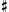and
C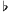
of the 19 tone system).
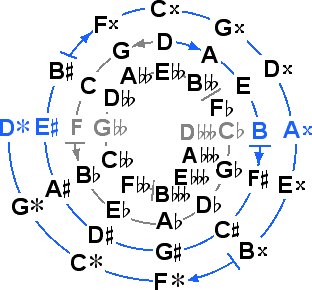
This interval between D and
D sounds much smaller than its raw staff size,
and in fact approaches the sound of a perfect fourth.
It is however systemically related to the augmented fourth F up to B from the diatonic naturals.
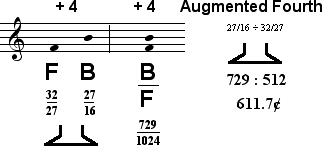
Juxtaposition of these intervals shows that sextupally diminishing an octave created an interval that is smaller than augmenting a fourth only once.
The fact that this sextupally diminished octave sounds almost as a perfect fourth in the 43 tone system is of great significance. Recall that the lack of a perfect fifth (or fourth) between the end tones F and B of the diatonic naturals is what necessitated accidentals (tritone correction). Now we find a system which mitigates this problem by supplying end tones which sound at almost a perfect fourth.
Between the end tones we also find other new intervals, sextupally diminished fifths, from
D up to A
and G up to D.
Sextuple diminishment turns these fifths into very small intervals, even smaller than the commas we have found elsewhere.
Yet they are related to the minor seconds from the diatonic naturals.
Comparison of these intervals side by side shows that sextupally diminishing a fifth creates a smaller interval than a minor second.
The placement of these sextupally diminished fifths within the scale show that the 43 tone system has special significance, with these two new intervals recalling the two diatonic halfsteps of the diatonic naturals.
The 43 tone system has 31 Pythagorean commas, whereas 31 tones has 19 commas, and 19 tones has 7 commas. The numerical pattern continues. While the letter names of the end tones of the 43 tone system suggest that this might be a good place to stop, and the introduction of triple accidentals might suggest that standard terminology is beginning to become a bit of a stretch, a yet larger system with a greater numbers of commas (you know how many), reveals other new and interesting interval qualities which prove also to be instructive, and exploring this larger system will help us decide just where the most logical stopping place is.
NEXT: 55 Tones