
With ratios containing up to a whopping 13 digits, the 55 tone system includes new quadruple accidentals which correspond to adjacent scale steps notated a sixth apart in terms of raw staff distance, as shown below.

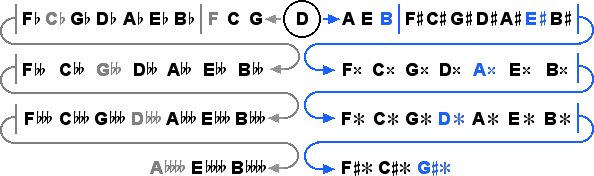

At the egdes of this system we find a septupally diminished second, between
G
 and
A
and
A
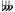 .
At this point the standard notation really starts to break down, but we will continue to find out
how these tones relate to the end tones F and B of the diatonic naturals, as well as
D
.
At this point the standard notation really starts to break down, but we will continue to find out
how these tones relate to the end tones F and B of the diatonic naturals, as well as
D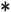 and D
and D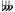 of the 43 tone system, G
of the 43 tone system, G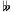 and
A
and
A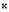 of the 31 tone system, and
E
of the 31 tone system, and
E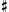 and
C
and
C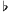 of the 19 tone system.
of the 19 tone system.



Considering this interval between
G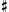
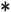 and
A
and
A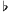
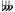 is tricky. We could try to arrange the notes as a seventh, so that
we have a septupally augmented seventh, but doing this results in an interval which is
larger than an octave. So, we arrange the notes as a second, but this
seven times diminished second has the bizarre characteristsic of so many of the scale
steps of these large scales, that is, of being notated in the opposite
direction that it sounds. So we have a second descending in notation, but an
interval of considerable distance ascending aurally. The quality does suggest that the sound and
the interval belong together as long as one can comprehend the necessary relocation of the note names,
but this becomes rather confusing particularly when trying to conceive of the interval harmonically.
is tricky. We could try to arrange the notes as a seventh, so that
we have a septupally augmented seventh, but doing this results in an interval which is
larger than an octave. So, we arrange the notes as a second, but this
seven times diminished second has the bizarre characteristsic of so many of the scale
steps of these large scales, that is, of being notated in the opposite
direction that it sounds. So we have a second descending in notation, but an
interval of considerable distance ascending aurally. The quality does suggest that the sound and
the interval belong together as long as one can comprehend the necessary relocation of the note names,
but this becomes rather confusing particularly when trying to conceive of the interval harmonically.

The interval sounds at nearly a perfect fifth, and this is of monumental significance. Consider that as the ends tones of the system this interval is systemically related to the augmented fourth F up to B from the diatonic naturals.


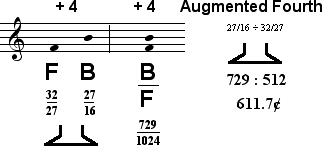
When we compare these intervals, we can hear how the single greatest systemic problem in the diatonic system - the lack of a perfect fifth between its outermost tones - is here almost miraculously done away with, as the ends of the system finally do correspond to a nearly perfect fifth, albeit one that is spelled as a septupally diminished second.




We also find other new interesting and significant intervals between the end tones of the system,
sextupally diminished sixths, from
C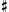
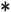 up to
A
up to
A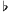
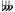 and
G
and
G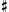
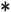 up to
E
up to
E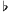
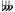 .
.


The sixths are diminished so much (six times) that the interval is virtually eliminated, resulting in an interval sounding a near unison.

Consider that these intervals are systemically related to the minor seconds of the diatonic naturals.



When we juxtapose these intervals, we find a very curious phenomenon. The minor seconds of the diatonic naturals literally converge into the near-unisons of the 55 tone system sextupally diminished sixths.




This convergence, or vanishing effect, is of paramount systemic significance. The two smallest intervals of the diatonic naturals have been virtually eliminated in the 55 tone system. When this is considered along with the appearance of the near-perfect fifth sounding from the septupally diminished second at the ends of the system, it becomes clear that this system represents a special stopping place.
The two sextupally diminished sixths in this system still clearly reflect the structure of the original diatonic naturals.



The 55 tone system has 43 Pythagorean commas, whereas the 43 tone system has 31 commas, the 31 tone syatem has 19 commas, and the 19 tone system has 7 commas. The numerical sequence is quite clear. But most importantly, this system reveals that a kind of progressive mutation has been occuring in all of these systems. In each next system, the ends of the system (related to F and B of the diatonic naturals) became closer and closer to sounding a perfect fifth, while the adjacent intervals (related to the halfsteps E to F and B to C of the diatonic naturals) became smaller and smaller, until with the 55 tone system, the ends sounds virtually a pure fifth, and the halfsteps have virtually vanished, sounding practically as unisons.
Considering this, we are prompted to tinker with the systems... If some intervals have virtually vanished, then why don't we just get rid of them? This way of thinking leads to a simplification of all of these systems through a process of elimination, explored just a bit in the final section of our scale explorations.
NEXT: Equal Divisions