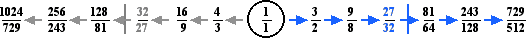
Consider the system of 13 tones, having one comma.
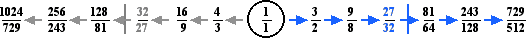

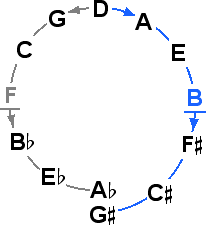
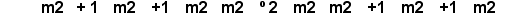
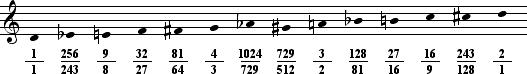
An idea suggested by the 13 tone system is to get rid of the difference between
G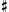 and A
and A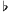 . This
means eliminating the diminished second - the comma
. This
means eliminating the diminished second - the comma 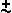 .
Since the comma is very close to 24 cents in size, and taking
these two tones and making them one leaves us with 12 tones, then all the fifths in the system
are intentionally mistuned or tempered by the same amount: (about 24)/12 = each about 2¢ flat.
This is the present-day ubiquitous and historically infamous tuning known as 12 tone Equal Temperament, or
12ET, in which every halfstep is exactly 100¢.
.
Since the comma is very close to 24 cents in size, and taking
these two tones and making them one leaves us with 12 tones, then all the fifths in the system
are intentionally mistuned or tempered by the same amount: (about 24)/12 = each about 2¢ flat.
This is the present-day ubiquitous and historically infamous tuning known as 12 tone Equal Temperament, or
12ET, in which every halfstep is exactly 100¢.

The above equation makes sense if one asks the question: what interval transposed up by its own distance twelve times is equal to an octave? Since transposition upwards in music is multiplication, to transpose an interval up by its own distance is to multiply an interval times itself; hence, we have some value times itself twelve times equalling 2. This would be shown by an exponent, and the inverse of this is the radical notation, shown above. On the right side of the equation is shown a shortcut from the actual linear value to the logarithmic units of cents.
In 12ET, there is no difference between diatonic and chromatic halfsteps, and pairs of sharps and flats which would normally be separated by a comma become the same pitch. The fifths are not far from pure, and the thirds are a fair approximation of their Pythagorean equivalents, but there is no trace of an harmonic mediant or submediant for producing pure sounding triads, which is considered by many to be its greatest deficiency. Other 12 tone tunings with improved (even perfect) thirds are a topic for another chapter yet to be written here. Because 12ET is the tuning is considered the default today, we will compare other systems below to it.
Next, we take another look at the 19 tone system.






One way of handling this system is simply to make all of the steps the same size, resulting in 19 Tone Equal Temperament, or 19ET.

This is a historically significant system advocated by many, perhaps most notably in the twentieth century by Joseph Yasser, although this tuning has advocates from centuries earlier. 19ET has very good thirds, but the fifths suffer a bit, and are actually worse than those of 12ET. Another way of dealing with the system is to eliminate the two doubly diminished thirds, and make all the remaining intervals the same size. This results in the system of 17 Tone Equal Tamperament, or 17ET, which has fifths that are a bit sharp, which sounds worse than them being flat, and thirds which are not so pleasant, both of which are worse than 12ET, although this system has also had its advocates.




Next we take another look at 31 tones. This system introduces double accidentals, which have been part of standard music theory for centuries.




As with 19, the first way of handling this system is simply to make all of the steps the same size, resulting in 31 Tone Equal Temperament, or 31ET.

This is a historically significant system which has good thirds and fifths, but the fifths are worse than 12ET. It has been especially used in Holland, having been the focal work of Adriaan Fokker. 31ET is a good choice for exploring expanded resources without having to expand present nomenclature, since only double accidentals are needed (although Fokker devised a system for 31ET having new and different accidentals). It is also possible to eliminate the two quadrupally diminished fourths, and make all the remaining intervals the same size, resulting in the system of 29 Tone Equal Temperament, or 29ET, in which the fifths are a bit sharp, though not as sharp at 17ET, and the thirds are fair, but also tuned on the wrong side, so it is not as favorable as 12ET, 19ET or 31ET.

Next we consider the 43 tone system. Recall that this system has special significance because the end tones are altered versions of the source tone creating a sextupally diminished octave which sounds almost a perfect fourth. This system introduces triple accidentals, which have been discussed theoretically for centuries but have not been made standard so far.

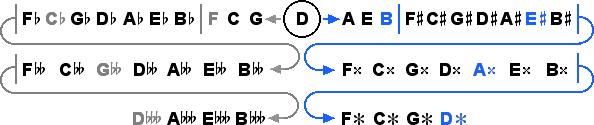
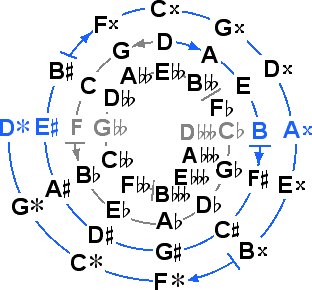

As with 19 and 31, the first way of handling this system is simply to make all of the steps the same size, resulting in 43 Tone Equal Temperament, or 43ET.

This is a system with rather flat fifths but fairly good thirds. The alternate method of handling the system works better in this case; by eliminating the two sextupally diminished fifths, the system of 41 Tone Equal Temperament, or 41ET, results.


This system has nearly pure fifths and good thirds, both better than 12ET, and the fifths are better than both 19ET and 31ET. 41 is ideal for expanding the present system using standard concepts only with the addition of triple accidentals.
Next, the system of 55 tones.

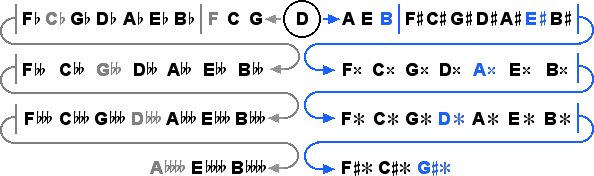


The system of 55 tones presents almost a natural elimination of two of its tones, the sextupally diminished sixths; therefore it is logical to carry through the elimination completely and make the remaining tones all equally spaced, so that we are left with the system of 53 Tone Equal Temperament, 53ET.

This system has excellent fifths and thirds, better than all the smaller systems. 53ET is historically very well known. It is only problematic to work with because it requires two degrees of expansion from our conventional system, as quadrupal accidentals are needed, such that it is rather unwieldy and difficult to manage. Considering that removing only three of the tones would rid the system of the quadruple accidentals, it seems a shame that this cannot be done as it would destroy the structure.
Our exploration of these Superscales leads us to some useful conclusions.
13 Tones
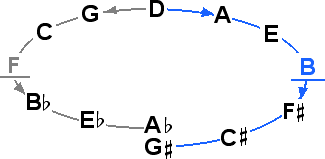
13 tones represents the first cycle approaching closure, which suggests our present system of 12ET. The fifths are good in 12ET but the thirds are not.
19 & 17 Tones
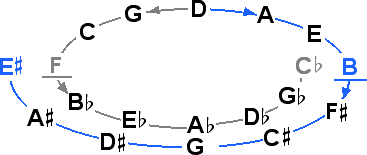
17ET and 19ET are both useful for working comfortably within a diatonic framework, as only sharps and flats are needed; 17ET has poorer thirds and fifths than 12ET, and 19ET has better thirds but poorer fifths than 12ET.
31 & 29 Tones

31ET is a good system requiring no expansion of existing concepts as it needs only double accidentals, only the fifth is poorer than 12ET.
43 & 41 Tones
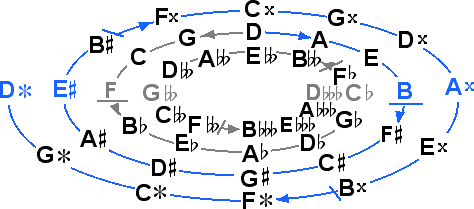
41ET has excellent fifths and good thirds, both better than 12ET, and it requires only the addition of triple accidentals to become practical.
53 Tones

53ET has the best fifths and thirds of all, and it represents a natural sort of stopping place. However, as it requires quadruple accidentals, it reaches just past managability without enough advantage to justify its use over 41, which maintains managability while still significantly improving both the fifths and thirds.
It should be mentioned that the diatonic structures at the heart of all of these systems can also be turned into equal systems, and these ETs are also useful and instructive.






Halfsteps and wholesteps of the diatonic naturals can be collapsed into a single step size, resulting in 7 Tone Equal Temperament, 7ET.

This tuning has a pleasant effect and is historically of note, being used in some parts of Asia and the Near East.



The tuning of 5 Tone Equal Temperament, 5ET, is a system used as much as 7ET, which also gives an amazing aural illusion of a pentatonic pattern even though the tones are equally spaced.

Our exploration has shown the extent to which our nomenclature can be reasonably applied to larger systems. It should be recalled that any tuning can be used to good effect, and thirds and fifths need not be the criteria for judging any given tuning.
The conclusions we have reached thus far provide background for a systematic expansion of the traditional Western system into a 41-tone paradigm. This topic is explored in complete detail in the next section.
NEXT: The Hunt System