
Although any number of units may be chosen, a logical choice should reflect the basic structure of the tones we are measuring. Consider the 13 tone system, shown below on the logarithmic ruler.

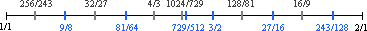
An examination of this system shows that all of the values fall very close to the tick marks of a tone ruler having 12 equal units, as shown below.

This tone ruler breaks the octave unit into 12 equal parts, not unlike the 12 inches of a foot ruler. The equation for the full length of our tone ruler is as follows.

Just as something measured with a foot ruler rarely matches up to a value of whole inches, so the tones of our system do not line up exactly with the 12 units of our tone ruler. For example, the interval 3/2 gives the following result.


Although 3/2 measures fairly close to a whole number of units, other intervals show greater discrepancies, such as 256/243.


The following values result for all 13 diatonic intervals.

Because we use a base 10 number system, our results show tenths and hundreths of units. Further subdivision of the 12 units would allow even more precise measurements to be made. Which subdivision would be a logical choice?
Although any number of subdivisions per unit may be chosen, our base 10 number system suggests that some multiple of 10 would be a logical choice. Alexander J. Ellis (1814-1890) popularized the use of 100 subdivisions per unit, so that the octave is divided into 1200 equal parts, logically grouped in hundreds, as shown below
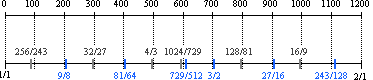
Each of these subdivisions Ellis called a cent. In most of the Western world, the cent (¢) is the standard unit for the measurement of distances between tones. The equation expressing the full distance of the cent ruler is given below.

When each of the tones of the 13 tone system is measured against the cent ruler, the following values result.

It is common to round cent measurements to the nearest tenth of a cent, as shown here.
How large of an interval ratio is a single cent? This can be shown by transforming the logarithmic equation into its expontential form and back again. Breaking the ruler into more than 1 unit requires the use of a fractional exponent.

The fractional exponent can be expressed using a radical.

The interval value for one cent is thus given as a decimal fraction.

This interval may then be expressed as a ratio.

This ratio can then be shown in the logarithmic equation with one cent as the resulting measure.

Distances between tones are easily found by adding or subtracting cent values. This is especially useful for measuring small intervals, such as the comma at the center of the 13 tone system.

The size of this comma in cents is 611.7¢ - 588.3¢ = 23.4¢

The cent ruler works very much like a normal ruler, allowing intuitive interval measurements to be made. The fact that the cent ruler is broken into 12 equal parts supplies a convenient analogy to the foot ruler, while the subdivision of each unit into 100 parts allows for simple calculations in our base 10 number system. In subsequent parts of this text, cent values are often cited.
NEXT: The last section of this chapter is intended for those interested in other units for measuring intervals. You may wish to move on to Chapter 5 · Triads