
This section is intended for those interested in other units for measuring intervals using some basic arithmetic. You may wish to move directly to Chapter 5 · Triads
The logarithmic and exponential expressions representing the tone ruler may be generalized using variables, as shown below.

The variables in these expressions have the following meanings.
 |
number of units on the tone ruler |
| full length of the tone ruler | |
| interval being measured | |
| interval size measured in Z units |
The following chart shows how the variables correspond between the two expressions.

Although the entire length of the ruler may be any interval, the octave serves as the default standard.

Although the interval x can be any real number, integer ratios may serve as a default.

Recall that the cent is the standard unit popularized by Alexander Ellis (1814 -1890). A new notation, Æ = 1200 can be used in place of Z to show how the cent appears in our general expressions.







Recall that this unit is based on the tonal organization of the 13 tone system.
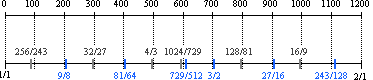
For this reason, the cent serves as a reference unit against which all other possible units are compared. Next, several other tone rulers are introduced, and each new unit is compared to the standard cent.
Joseph Sauveur (1653 -1716) and Felix Savart (1791 -1841), living more than a century apart, independantly developed a unit which provided ease of calculation. Sauveur called the unit an epiméride. This unit has since come to be known as the Savart.

The number 301 was a practical choice for purposes of quick calculations during a time when logarithms had to be looked up on tables, since the logarithm of 2 is 0.301029996... The 301 division reflects a 43 unit division, with each unit broken into 7 parts.







Augustus De Morgan (1806 -1871) developed a unit called the Jot, which takes the idea of the Savart to a higher level of precision. The jot represents a rounding of the logarithm of 2 to 5 decimal places: 0.301029996...
















NEXT: Chapter 5 · Triads