
The Dorian mode is derived according to melodic intervals and notated in harmonic intervals below.




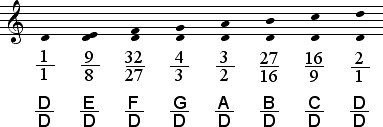

The order of letters above is used explore the intervals of each mode, first moving away from the center D to the right in the order D A E B, and then moving away from the center D to the left in the order G C F. As the central tone shifts from the center D to the right, the number of intervals which are smaller is increased. As the central tone departs from the center D to the left, the number of intervals which are larger is increased.
By shifting the central tone from D to A, the Aeolian mode is created.




In the Aeolian mode the Sixth 16:27 is replaced by a smaller Sixth 81:128.



By shifting one more fifth to the right, from A to E, two intervals differ from those of Dorian.




The Sixth 16:27 is replaced by 81:128, just as in Aeolian. Additionally, the Second 8:9 is replaced by a smaller Second 243:256 in the Phrygian mode.



Shifting one more fifth to the right, from E to B, results in three intervals differing from those of Dorian.




In Locrian, the Sixth 16:27 is replaced by 81:128, just as in Aeolian. The Second 8:9 is also replaced by 243:256, just as in Phrygian. Finally, Locrian is the only mode in which the Fifth 2:3 is replaced by a smaller Fifth 729:1024.



With the Locrian mode centered on B, we reach one of the natural limits of the diatonic system.
We now venture in the opposite direction from the central tone D. By shifting the central tone from D to G, the Mixolydian mode is formed.




The Third 27:32 is replaced by the larger Third 64:81.



By shifting one more fifth to the left, from G to C, two intervals differ from those of Dorian.




Just as in Mixolydian, the Third 27:32 is replaced by 64:81. Additionally, the Seventh 9:16 is replaced by the larger Seventh 128:243 in the Ionian mode.



Shifting one more fifth to the left, from C to F, results in three intervals differing from those of Dorian.




The Third is altered from Dorian's 27:32 to 64:81, just as it is in Mixolydian and Ionian. The Seventh is also replaced by 128:243 just as it is in Ionian. Finally, Lydian is the only mode in which the Fourth 3:4 is replaced by the larger Fourth 512:729.



With the Lydian mode centered on F, we reach one of the natural limits of the diatonic system.
The following table shows all the natural harmonic intervals for each mode in notation and in ratios. The arrangement of modes follows the order given above, beginning with the center D Dorian and moving out by fifths towards B Locrian, increasing the number of smaller intervals, and then returning to the center D and moving to the left towards F Lydian, increasing the number of larger intervals. Dorian intervals and intervals of other modes which differ from those of Dorian are shaded.
 | ||
| D Dorian | 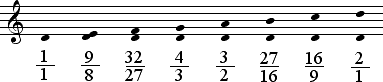 |
|
| A Aeolian | 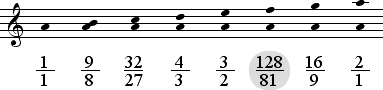 |
|
| E Phrygian |  |
|
| B Locrian |  |
|
| D Dorian | 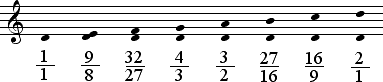 |
|
| G Mixolydian | 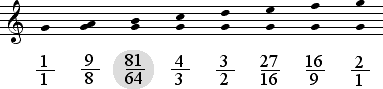 |
|
| C Ionian | 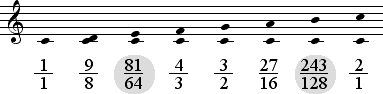 |
|
| F Lydian |  |
The table below shows the seven modes arranged symmetrically around Dorian. The tonic letter name of each mode is shown at the left. Dorian is surrounded by modes having increasing numbers of smaller or larger intervals as indicated at the right.
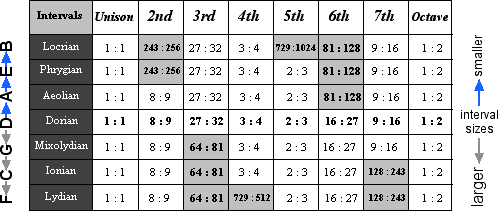
We may observe from the table above that the leftmost and rightmost columns headed Unison and Octave contain only one value each, whereas the other columns contain more than one value. Further inspection shows that there are exactly two values per column. This means that while there is only one natural Unison and only one natural Octave, there are two kinds of natural Seconds, Thirds, Fourths, Fifths, Sixths, and Sevenths. These two kinds of natural intervals are classified by what are called interval qualities, explained in the next section.
NEXT: Interval Qualities