
Before discussing interval qualities, two broad categories of intervals are defined. Recall the three primary tones of the Western diatonic system: the tonic, the dominant, and the subdominant.

In diatonic arrangement, intervals between these tones occur at the first, fouth, fifth, and eighth positions of the Dorian mode.
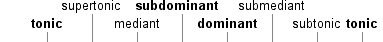

Recall that the names of the tonic, dominant, and subdominant reflect the primary role they play in the structure of the Western diatonic system. The intervals resulting from these tones are called Perfect. These are the only intervals which receive this epithet.

Each of these intervals has a straighforward, strong, simple sound. The designation Perfect thus further emphasizes the basic structural significance of the tonic, dominant, and subdominant tones. As one might expect, the remaining intervals are classified as Imperfect. These are the Seconds, Thirds, Sixths, and Sevenths.

Recall the table below, which summarizes the natural harmonic intervals expressed in ratios for all modes.
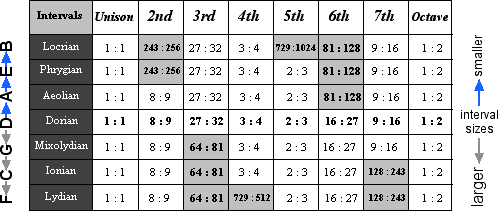
Again note that the leftmost and rightmost columns headed Unison and Octave contain only one value each, whereas the other columns contain exactly two values per column. While there is only one natural Unison and only one natural Octave, there are two kinds of natural Seconds, Thirds, Fourths, Fifths, Sixths, and Sevenths. The two kinds of intervals in each column are designated by interval quality.
The qualities of natural intervals may be summarized by compaing the Dorian mode with the Lydian and the Locrian mode.
| Locrian |  |
| Dorian |  |
| Lydian |  |
Because Dorian is at the center of the system while Lydian and Locrian are at the extreme ends of the system, these three modes taken together contain all of the natural interval qualities within the octave, as shown in the table below.
These three modes are shown below in notation with ratios. Lydian and Locrian intervals which differ from those of Dorian are shaded just as they are in the table above.
 | ||
| B Locrian |  |
|
| D Dorian | 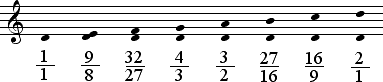 |
|
| F Lydian |  |
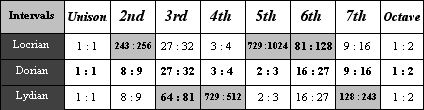
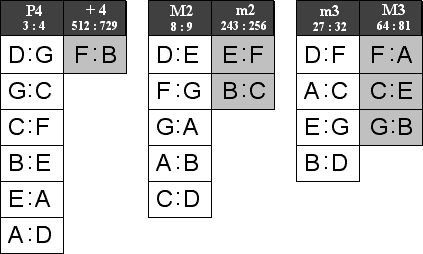
If we compare only the Perfect intervals, that is, the columns for the Unison, Fourth, Fifth, and Octave, we see only one type for the Unison and Octave, and two types for both the Fourth and the Fifth. The table below shows only the columns for the Perfect intervals.
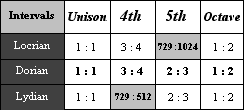
The differing distances of the Fourths and Fifths given by the values in the table are shown in the figures below. The Fourth 512:729 is larger than the Fourth 3:4.

When an interval normally classified as perfect is larger than the natural perfect version, the quality of the larger interval is called augmented. Thus the Fourth 512:729 in Lydian is called an Augmented Fourth while the Fourth 3:4 in Dorian is a Perfect Fourth. The letter P preceeding an interval number indicates a Perfect quality while a plus sign + indicates an Augmented quality.
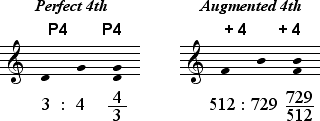
Likewise, the Fifth 729:1024 is smaller than the Fifth 2:3.

When an interval normally classified as perfect is smaller than the natural perfect version, the quality of the smaller interval is called diminished. Thus the Fifth 729:1024 in Locrian is called a Diminished Fifth while the Fifth in Dorian 2:3 is called a Perfect Fifth. A degree symbol ° indicates a Diminished quality.

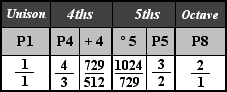
The qualities of the diatonic perfect intervals are summarized in the table below.
Diatonic Perfect Intervals
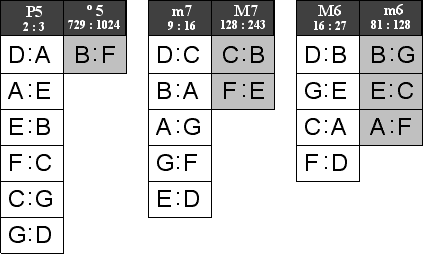
Comparing the imperfect intervals of the Dorian mode with those of the Lydian and Locrian modes shows two kinds of Seconds, Thirds, Sixths, and Sevenths.
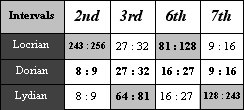
The two sizes of imperfect intervals have been classified throughout history in various languages simply as large or small. The modern terms for these two sizes are called Major and Minor, respectively. A lowercase letter m preceeding an interval number indicates a Minor quality while an uppercase M indicates a Major quality. The differing distances for each pair of imperfect intervals are shown in the figures below. The Second 243:256 is smaller than the Second 8:9. Therefore, the Dorian Second 8:9 is called a Major Second while the Locrian Second 243:256 is called a Minor Second.

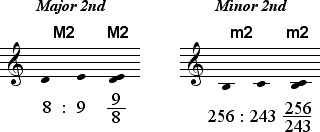
The Third 27:32 is smaller than the Third 64:81. Therefore, the Dorian Third 27:32 is called a Minor Third while the Lydian Third 64:81 is called a Major Third.

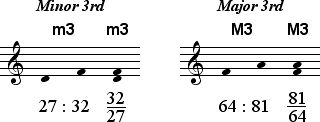
The Sixth 81:128 is smaller than the Sixth 16:27. Therefore, the Dorian Sixth 16:27 is called a Major Sixth while the Locrian Sixth 81:128 is called a Minor Sixth.

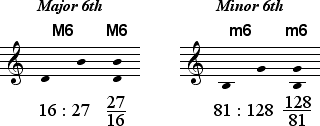
The Seventh 9:16 is smaller than the Seventh 128:243. Therefore, the Dorian Seventh 9:16 is called a Minor Seventh while the Lydian Seventh 128:243 is called a Major Seventh.

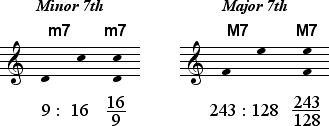
The qualities of the diatonic imperfect intervals are summarized in the table below.
Diatonic Imperfect Intervals
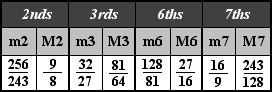
The following table shows all of the qualities of the natural harmonic intervals for each mode. Intervals differing in quality from those of Dorian are shaded.
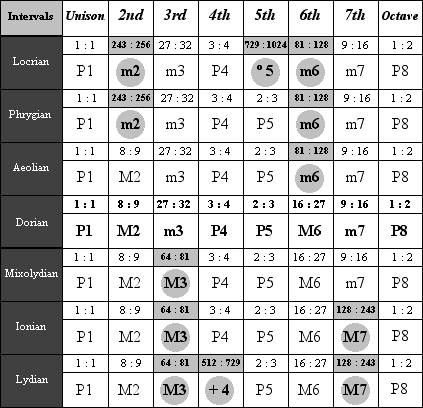
If we examine all of the intervals included above, we see a total of 13 different values. These 13 intervals are known as the diatonic intervals, as shown in the table below.
13 Diatonic Intervals

The table below shows all of the natural the modes in notation with interval qualities.
| D Dorian |  |
|
| A Aeolian |  |
|
| E Phrygian |  |
|
| B Locrian |  |
|
| D Dorian |  |
|
| G Mixolydian |  |
|
| C Ionian |  |
|
| F Lydian |  |
Having established the qualities of natural intervals by ratios and notation, we return to the expression of tones as letters. The table below shows the natural tones of each mode expressed as letters. Tones which differ from those of Dorian are shaded.
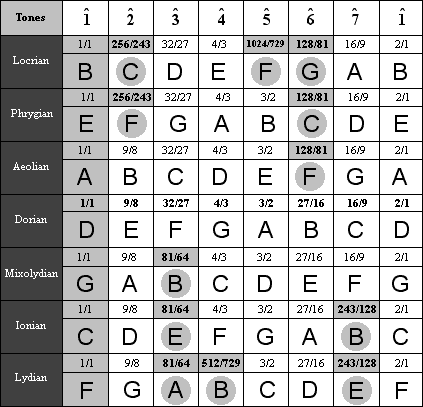
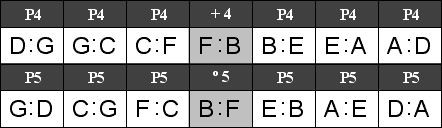
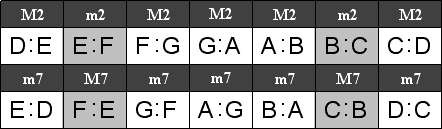
Having recalled all of the natural tones as letters, below we arrange the natural intervals by size and quality, expressed in letters. Unisons and Octaves are left out, because these intervals are always perfect when only natural letters are used. Interval qualities are thus given by letters alone, and musicians must know the qualities of intervals based on letters alone. To learn interval qualities by letters alone, the tables below should be memorized.
The center of the system D serves as the first and last letter in the left half of each column. The two rows of three columns each show inversional relationships above and below; for example, Fourths are placed above Fifths to show that these intervals are inversions of each other. The qualities of each interval are also arranged so that inversions are placed in the same half of each column; for example, Minor Thirds are inversions of Major Sixths. The inversional relationships may also be seen in the numbers which make up the interval ratios as well as the letter names of the tones; for example, the Major Sixth 16:27 is the inversion of the Minor Third 27:32, which may be expressed as D:B inverting to B:D.
The cyclical structure of the natural interval qualities may be emphasized by arranging the naturals in an arch to show the discontinuity between the extremes of the system; F and B.

The Perfect Fourths and Fifths can be arranged cyclically around the central Augmented Fourth and Diminished Fifth.
A cycle of Major and Minor Seconds and Sevenths shows symmetry with D at the ends and G and A in the middle.
The Major and Minor Thirds and Sixths form an alternating cycle, again showing symmetry around D.
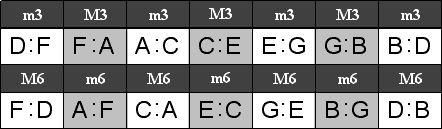
The cyclical structures of the interval qualities are summarized in the table below, which uses only shading to show qualities according to the tables above, and shows inversions simply as a change of direction from left to right.

This concludes our study of the system of diatonic natural tones, letters, notes, modes and intervals. Further exploration of the system begins by adding more tones, which requires the introduction of accidentals.
NEXT: Chapter 3 · Accidentals