
In this chapter, diatonic intervals are derived and demonstrated melodically and harmonically.
The Dorian mode serves as the center of the modern diatonic modal system. It is a symmetrical arrangement of seven tones, as derived in Chapter 1.



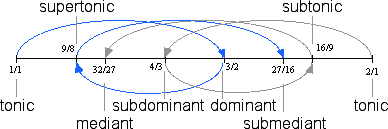


In Western music, the term mode has complex implications, and historically speaking modes are a tremendously complicated matter; however, the modern diatonic modes are just simple permutations of the seven natural tones, and the arrangement of letters around D can serve as the roadmap for our tour of the modern diatonic modes. Below, these modes are introduced in order according to the Dorian arrangement, first moving away from the center D to the right in the order D A E B, and then moving away from the center D to the left in the order G C F. As the central tone shifts from the center D to the right, the number of tones which are lower in relation to the tonic is increased. As the central tone departs from the center D to the left, the number of tones which are higher in relation to the tonic is increased.
By shifting the central tone from D to A, in the Aeolian mode is created.




The submediant 27/16 is replaced by the lower tone 128/81.




By shifting one more fifth to the right, from A to E, two tones differ from those of Dorian.




The submediant 27/16 is replaced by 128/81, just as in Aeolian. Additionally, the supertonic 9/8 is replaced by the lower tone 256/243 in the Phrygian mode. This tone is sometimes called flat 2.




Shifting one more fifth to the right, from E to B, results in three tones differing from those of Dorian.




In Locrian, the submediant 27/16 is replaced by 128/81, just as in Aeolian. The supertonic 9/8 is also replaced by 256/243, just as in Phrygian. Finally, Locrian is the only mode in which the dominant 3/2 is replaced by the lower tone 1024/729. This tone is sometimes called flat 5.




With the Locrian mode centered on B, we reach one of the natural limits of the diatonic system.
We now venture in the opposite direction from the central tone D.




By shifting the central tone from D to G, the Mixolydian mode is formed. The mediant 32/27 is replaced by the higher tone 81/64.




By shifting one more fifth to the left, from G to C, two tones differ from those of Dorian.




Just as in Mixolydian, the mediant 32/27 is replaced by 81/64. Additionally, the subtonic 16/9 is replaced by the higher tone 243/128 in the Ionian mode. This tone is no longer referred to as the subtonic, but has rather been given the name leading tone, due to its closer proximity to the tonic which is said to lead the ear towards the tonic.




Shifting one more fifth to the left, from C to F, results in three tones differing from those of Dorian.




The mediant is altered from Dorian's 32/27 to 81/64, just as it is in Mixolydian and Ionian. The subtonic is also replaced by the leading tone 243/128 just as it is in Ionian. Finally, Lydian is the only mode in which the subdominant 4/3 is replaced by the higher tone 729/512, which is not called the subdominant, but rather has been dubbed the tritone (because it spans 3 wholesteps which are also known as tones), and is also sometimes called sharp 4.




With the Lydian mode centered on F, we reach one of the natural limits of the diatonic system.
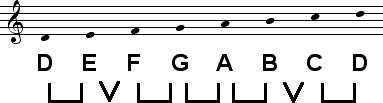
Each mode is shown below in notation with ratios and wedges showing halfsteps. The modes are presented as above, in fifths order, first moving away from the center D to the rightmost extreme B, increasing the number of tones which are lower in relation to the tonic, and then returning to the center D and moving to the leftmost extreme F, increasing the number of tones which are higher in relation to the tonic. Dorian tones and tones of other modes which differ from those of Dorian are shaded.
 | ||
| D Dorian |  |
|
| A Aeolian |  |
|
| E Phrygian |  |
|
| B Locrian |  |
|
| D Dorian |  |
|
| G Mixolydian |  |
|
| C Ionian |  |
|
| F Lydian |  |
The table below shows the seven modes arranged symmetrically around Dorian. The tonic letter name of each mode is shown at the left. Dorian is surrounded by modes having increasing numbers of lower or higher tones as indicated at the right.

A similar table is given below, showing scale degree names instead of tone ratios. Only degrees which differ from those of Dorian are shaded.

Thus far we have discussed each tonal arrangement as a succession of individual tones in ascending scale order. Next we will look at how each tone relates as a harmonic interval with the tonic of each mode.