
Intervals produced below the tonic are given the prefix sub. This is one way to lead to the idea of a subharmonic series, or a series of harmonics produced below the tonic rather than above it. Such a series is given below, with harmonic numbers shown upside down to emphasize the mirror relationship of this sub-series to the conventional harmonic series.
Subharmonic Series

Subharmonics 4, 5 and 6 together form a Minor Triad.
Subharmonics 4:5:6

When placed within the boundaries and changed to conventional ratios, the tones of the minor triad are 2/1, 8/5, and 4/3.


These three tones are the tonic, the harmonic submediant, and subdominant.
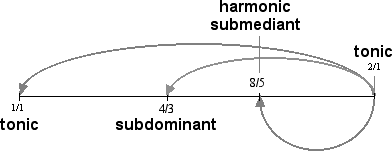
The tone 8/5, considered from this inversional orientation, is a third away from the upper tonic; however, the term Minor in Minor Triad refers to the quality of the interval above the lowest tone, which is the subdominant. This is a new Minor Third which is slightly larger than the Pythagorean m3, 27:32, so it may be called the Large Minor Third, or Lm3. This larger third is also called the Just Minor Third.

The minor triad also contains a Perfect Fifth, 2:3, and a Small Major Third, 5:4 is incidentally found between the two upper tones of the triad.

Contrary to the implications of the subharmonic series, the tones of the minor triad are named following the form of the major triad; the lowest tone is called the root, and the tones above the root are known as the third and fifth.
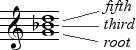
The minor third is a controversial interval in music theory; however, unless otherwise specified, the third of a minor triad may be assumed to be the large minor third 5:6 rather than the Pythagorean minor third 27:32.