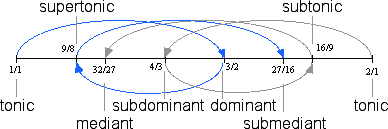
Recall the 13 diatonic intervals shown in the table below.
We discovered these thirteen intervals by exploring the diatonic modes. By mixing together all of the modes, using sharps and flats, all of the intervals shown above may be represented as a single thirteen tone system, as shown below.
We begin with the 7 natural tones.
The notation below shows larger horizontal gaps between the five diatonic wholesteps, with some extra space in the middle. This extra space will be filled in with notes having sharps and flats.
In the natural diatonic system, two diatonic halfsteps are available. As tones are added, more halfsteps become available.
Recall that moving away from the tonic one step to the right or to the left results in the Aeolian and Mixolydian modes respectively, each of which differ from Dorian by one tone.
| Aeolian |  |
In Aeolian, a lower submediant is introduced.
| Mixolydian | 
|
In Mixolydian, a higher mediant is introduced.
When these alternate mediant and submediant tones are added to the Dorian system, a total of nine tones results.
The two types of mediants and submediants are designated major and minor.
The higher mediant becomes a sharp note, and the lower submediant becomes a flat note.
Thus, our first sharp note is F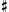
, and our
first flat note is B
.
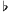With the addition of B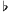 and F
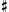, four diatonic halfsteps are available.
Two qualities of sixths and thirds become available above the tonic.
Moving away from the tonic two steps to the left or to the right results in the Ionian and Phrygian modes respectively, each of which differ from Dorian by two tones.
| Ionian |  |
In Ionian, the leading tone replaces the subtonic as a higher seventh scale degree.
| Phrygian | 
|
In Phrygian, the flat 2 replaces the supertonic as a lower second scale degree.
The leading tone and the flat 2 are added to the system when these two modes are combined together with Dorian, resulting in a total of eleven tones.
The raised seventh degree becomes a sharp note, and the lowered second degree becomes a flat note.
Thus, the second sharp note to be added to the system is C
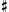, and the second flat note is E
.
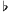With the addition of E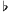 and C
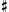, six diatonic halfsteps are available.
Two qualities of seconds and sevenths become available above the tonic.
Moving away from the tonic three steps to the left or to the right results in the Lydian and Locrian modes respectively, each of which differ from Dorian by three tones.
| Lydian |  |
In Lydian, the sharp 4 replaces the subdominant as a higher fourth scale degree.
| Locrian |  |
In Locrian, the flat 5 replaces the dominant as a lower fifth scale degree.
When the sharp 4 and the flat 5 are added to the Dorian system, a total of thirteen tones results.
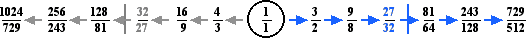
The raised fourth degree becomes a sharp note, and the lowered fifth degree becomes a flat note. This results in the counterintuitive notation of a higher tone by a note which is placed lower on the staff.
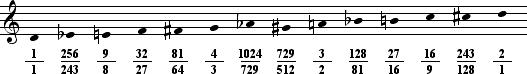
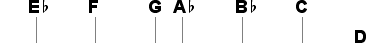
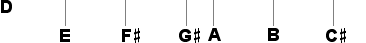
Thus, the third sharp note to be added to the system is G
, and the third flat note is A
.
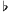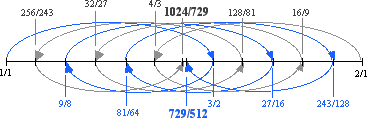
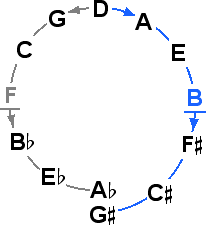
This 13 tone chain of fifths can be shown in the form of a spiral.
With the addition of A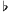 and G
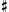, eight diatonic
halfsteps are available.
Two qualities of fifths and fourths become available above the tonic.
By mixing together all of the modes, using sharps and flats, all thirteen diatonic intervals are available above a single tonic.
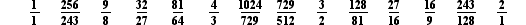
The 13 tone spiral illustrates that the tones labeled G
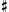and A
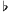are very close to the same value. The small interval between these two tones is called
a Comma, which comes from a Greek word meaning a small piece which is cut off.
More specifically this is the Pythagorean Comma, because our tuning is based on the
3-limit of the Pythagoreans. This comma may also be called a Fifths Comma, as the
3 limit corresponds to tuning in pure fifths.
This is not the only comma we will enounter. Next we see how intervals such as the comma are measured using a unit called cents.
NEXT: Chapter 4 · Measurement