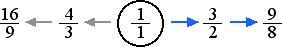
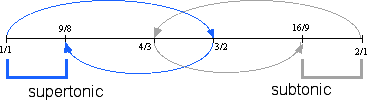
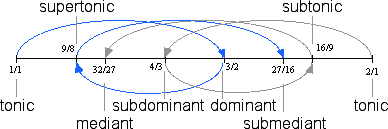
How do we produce more tones without going beyond the 3-limit? The simplest solution is to use each of the new tones to produce another new tone. Recalling that the first new tone is related by 3, we use the relation to produce two new tones symmetrically around the source tone. This means creating relations of 3 times 3, which is 9. On the one hand we have 9/1 above the source tone and on the other we have 1/9 below the source tone. To justify these tones, we find duplicates by successively multiplying and dividing by 2. This gives 9/8 above, and 16/9 below the source tone.
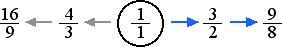
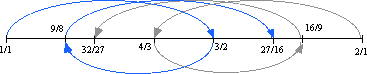
These two new tones are inversions of each other. The figure above shows how these new tones are produced symmetrically, and the number line below reflects how we hear these new tones along with the others within the boundary tones.
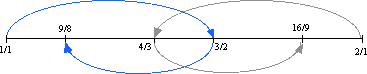
9/8 is equal to 1 and 1/8, or 1.125 as a decimal fraction, and 16/9 is equal to 1 and 7/8, or 1.77 as a decimal fraction, as shown below on a typical number line.
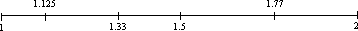
The names of these two new tones are derived from their proximity to the tonic. One is directly above the tonic and the other is directly below it. The prefix super means above and, as stated earlier, the prefix sub means below; hence, these two new tones are called the supertonic and subtonic respectively. Just like the dominant and subdominant, the names of this pair of tones reminds us that they are inversions of each other.
The figure below summarizes the names of the tones derived so far.
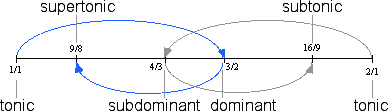
At this point, we have derived a collection of tones which is in fact found in a wide range of folk musics from around the world. These five tones are known as pentatonic; penta means five in Greek. Pentatonic music has a recognizable sound, resulting directly from the intervals, the distances between the tones, in the system. The smallest interval between any two tones in a pentatonic system is 8:9, which appears in three places.
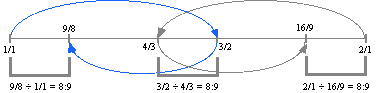
Notice that an interval, the distance between two tones, is found by dividing the higher tone by the lower tone, and the result is expressed with a colon in the form lower : higher. This form is used to distinguish intervals from tones, which are expressed with a slash in the form higher / lower. The interval 8:9 is significant, and a bracket-like figure is often used to represent this interval.
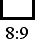
Why stop at five tones? We can still produce more tones. Again, the simplest method is to use each of the new tones to produce another new tone. We use the relation 3 to produce two new tones symmetrically around the source tone, which means creating relations of 3 times 9, which is 27. On the one hand we have 27/1 above the source tone and on the other hand we have 1/27 below the source tone. To justify these tones, we successively multiply and divide by 2. This gives 27/16 above, and 32/27 below the source tone. These two tones are inversions of each other.
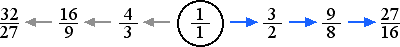
27/16 is equal to 1 and 11/16, or 1.6875 as a decimal fraction, and 32/27 is equal to 1 and 5/27, or 1.185 as a decimal fraction, as shown below on a standard number line.
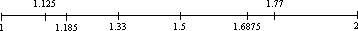
The names of these two new tones correspond to thier proximities to the tonic tones and the dominant tones. The tone 32/27 is roughly in the middle between the tonic and the dominant, while the tone 27/16 is roughly in the middle between the upper tonic and the subdominant. The word mediant means middle. 32/27 is the called the mediant while 27/16, being between then tonic and subdominant, is called the submediant. Again the names of this pair of tones reminds us that they are inversions of each other.
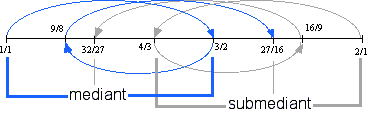
The figure below summarizes the names of all of the tones we have derived.
At this point, we may notice that the number line is getting fairly crowded. A small interval appears between 9/8 and 32/27, and also between 27/16 and 16/9.
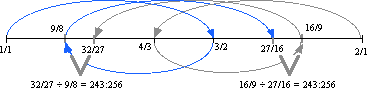
The appearance of this smaller interval, 243:256, marks an arrival point, and a temporary stopping place for the derivation of our system. A wedge-like figure is used to represent this interval.
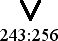
These seven tones are considered a complete group. The two symbols of the bracket and the wedge can be used to show two different intervals from one tone to the next.


These seven tones are called natural tones, or simply naturals. The brackets and wedges designate intervals which at this point we can call steps. The two sizes of steps are given the following names which roughly describe their approximate relationships to each other.
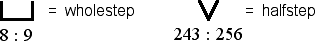
Sounding all seven of the natural tones in sequence is considered to have stepped through the tones. The term diatonic literally means through tones in Greek; hence, this is known as a diatonic arrangement of tones. The modern ordering of tones from lowest to highest is known as a scale; hence, this arrangement is also known as a diatonic scale.
Beginning with the 3 Tones, we have derived four new tones in a symmetrical arrangement, creating a diatonic scale of seven tones.
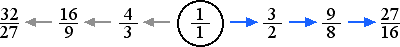

Our next task is to come up with simple ways to represent the tones using letters and symbolic notation.
NEXT: Letters & Notation