
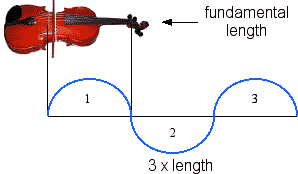
How do we find a new tone which is not a duplication? We know such a tone cannot be an even number. Since we have started counting with our first two tones, 1 and 2, we simply keep counting, and arrive at the number 3, which is the first odd prime. If the string is touched and bowed at a point one third of the way along the neck of the viola, a new pitch is produced.

This is called the third harmonic in the harmonic series. The three arcs below show that the string is broken into thirds.
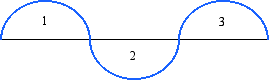
Although this new pitch is clearly related to the pitch produced by the entire string, it is also clearly not a duplication of it. The vibrating segment is one third as long as the whole string, so we can call this segment 1/3. This segment also vibrates 3 times as fast as the first tone. The figure above is shown in blue to signify that the number 3 represents the first new tone. The value of this tone, 3, is obviously larger than 2. To justify this tone, we use the relationship of duplication, dividing the tone by 2, which gives us 3/2, a congruence of 3 which sounds lower in pitch.
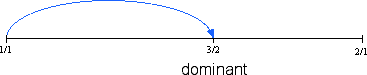
Having justified this new tone, we can see how it fits within the boundary tones. The figure below signifies that the new tone was derived from the source tone. The number line below the figure reflects how we hear the new tone in terms of its distance from the boundary tones.
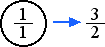

3/2 is equal to 1 and 1/2, or 1.5 stated as a decimal fraction, shown below on the common linear number line.
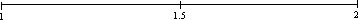
As the first new tone, the tone 3/2 has a prominant function within the structure of the Western system. The significance of this tone is reflected in the name given to it by music theorists; it is called the dominant.
The figure below summarizes the names of the tones we have derived so far.

The third harmonic expanded the system with a new tone. How are more tones added? First, we simply try counting. We reach the number 4, bringing us to the fourth harmonic in the harmonic series, which may be produced by touching and bowing the string at one fourth of its entire length.

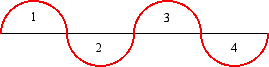
The arcs show the string broken into four sections. Because 4 is 2 x 2, this tone is a duplication of the second harmonic, which in turn was a duplication of the first harmonic, or fundamental. So, unfortunately this tone does not expand the system.
Symmetry is an appealing property of many natural forms. So far, we have derived an asymmetrical system, as shown below.


A tone must be added to make the system symmetrical. How is this done? Consider that the relationship between the first new tone 3 and the first tone 1 is 3/1, which becomes 3/2 when placed within the boundaries of 1 and 2. If we use this relationship in reverse, we create symmetry around the source tone. This new tone is not produced by a segment 1/3 as long as the entire string, but rather is produced by a string 3 times as long as the original fundamental.
Just as a shorter length resulted in a higher pitch, a longer length results in a lower pitch.
This new string does not vibrate 3 times as fast as the source tone, but rather 1/3 as fast. To justify this tone, we have to multiply it by 2, twice, so that 1/3 becomes 2/3 and then 4/3, becoming higher in pitch with each duplication.
Just as the first new pitch 3/2 was initially produced above the source tone, this new pitch 4/3 was initially produced below it. This above versus below relationship is called inversion. Just as 3/2 is shown with an arrow pointing to the right from the lower tonic, its inversion 4/3 is shown with an arrow pointing in the opposite direction from the higher tonic.
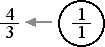

The figure below shows the symmetrical relationship between 3/2 and 4/3. These two tones, 3/2 and 4/3, are inversions of one another.
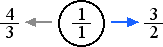

4/3 is equal to 1 and 1/3 or 1.33 stated as a decimal fraction, shown on the common number line below.
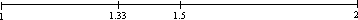
Just as the first new tone 3/2 is derived above the tonic 1/1, so the symmetrical tone 4/3 is derived below the tonic 2/1. The name given to this second new tone is the same as the first, with the prefix sub which simply means below; it is called the subdominant.
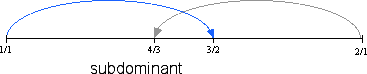
The figure below summarizes the names of the tones we have derived so far.

Since 2/1 is a duplication of 1/1, we have three non duplicate tones. These three tones form the backbone of the Western tonal system. For this reason, the intervals, or distances between the tonic and each of the other tones, are called Perfect. No other intervals receive this epithet.
Before moving on, we can review how the system has been derived so far. We have used a string on a viola, bowing the string at its entire length, at 1/2 of this length, at 1/3 of this length, and at 1/4 of its entire length.

The tones thus produced are the first four harmonics, numbered 1, 2, 3 and 4, of the harmonic series. Only the third harmonic results in a tone which is not a duplication of the first harmonic, which is the source tone or fundamental. This relationship is used to build two new tones which are symmetrically justified around the source tone. These two symmetrical tones together with the source tone constitute the three most important tones of the Western system.

The importance of these tones is reflected in the names music theorists have given to them. The names given here were popularized during the 18th century and are standard today. To summarize, the source tone is called tonic, which means tone in Greek, the first new tone above the tonic is called the dominant, and its symmetrical counterpart below the tonic is called the subdominant, meaning the dominant below. The dominant and subdominant are inversions of each other. The names tonic, dominant and subdominant logically reflect both the derivation and the function of each tone as the most important in the Western system.

The figure below shows overlapping patterns for the first four harmonics. This figure can serve as a reminder that when the entire length of a string is made to vibrate without touching the string at any point, the string vibrates in all its harmonics at once.
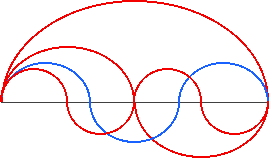
Although the freely vibrating string produces harmonics well beyond 4, the first four harmonics are all we need to complete our system. Since 3 is the only tone within this limit which is a new pitch, we call this a 3 limit system.
How can we produce more tones without going beyond the 3-limit? Try to answer this question on your own before going on.
NEXT: 5 & 7 Tones