
In this chapter, the simple structural foundation of tones, letters, numbers, and notation of the Western system, known as the scale of diatonic naturals, is derived.
Where do we begin? If zero (0) is the void, then the number one (1) represents the beginning. In music, this means the first tone. Such a tone can be produced as a pitch by plucking a string which has been placed under tension; this was the method used by the ancient Greeks. We can use a modern viola, and instead of plucking the string, we can use the bow to sustain the tone. [NOTE: Each audio example is a specifically tuned MIDI file.]

We can call the tone representing the whole vibrating length 1. This is called the fundamental or first harmonic of the musical harmonic series. The figure below shows a line with an arc across it. The line represents the viola string. The arc represents the vibration of the entire length of the string.

We can view this as the source tone from which all other pitches are derived. To show the primary function of this tone, we use the Greek word tonic, which simply means tone. The figure below can be used to signify the central function of the tonic.

tonic
What next? We simply count. The whole string is 1 part, and next we divide the string into 2 parts. We touch and bow the string at one half its entire length, producing another pitch.

When we try to match this pitch with our voices, we find that it is higher than the first, but it sounds almost exactly like the first. It has a feeling of maximal similarity about it. The string is divided into 2 segments. The vibrating segment is half as long as the whole string, so we can call this vibrating segment 1/2, which is what the Greeks did. It also turns out that this segment vibrates 2 times as fast as the first tone, and this is the preferred modern way to discuss these relationships. Either way, you can see that the number 2 represents maximal similarity for two tones. We can call this property congruence. This new tone is literally a doubling of the source tone, so we can also call the congruent tone a duplication. Additionally, it is also called the second harmonic in the harmonic series.
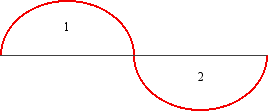
The two arcs show the string divided in two halves. All pitches related by 2 are congruent with one another; therefore, to find a congruent tone from any given tone, we simply multiply or divide the given tone by 2 any number of times. We can also observe at this point that all numbers which are divisible by 2 create tones which are duplications of lower numbers. The converse of this is that all numbers which are not divisible by 2 create tones which are not duplications. These numbers give us new tones. Such numbers are odd primes. The significance of this is made more clear below.
What is the significance of congruence, or duplication? The special relation between the source 1, and the pitch of maximal similarity, 2, serves as a standard against which all other pitches may be judged. So, we can call the congruent tones 1 and 2 boundaries for all other tones. This means that any other tone should have a value that lies somewhere between 1 and 2. Because 2 is related to the tonic by congruence, or duplication, it is also called tonic.

Because there are no whole numbers between 1 and 2, tones within these boundaries will have fractional values. These values can be shown on the number line. The number line above uses the base 10 linear system of decimal fractions, meaning that, for example, the value 1.5 would be placed exactly at the midpoint between 1 and 2; this scale represents how we normally think about numbers. In contrast, the number line shown below is base 2 logarithmic scale which uses whole number ratios, meaning that 1 and 2 are expressed as 1/1 and 2/1, and, for example, the value 3/2 would be used instead of 1.5, placed slightly to the right of center. The word logarithm comes from two Greek words meaning ratio number. Base 2 logarithmic measurements are closer to the way we hear pitches relative to one another.

These two number lines represent very different ways of measuring. Two charts below show the values 1 through 8 in both systems of measuring. Whereas the Base 10 Linear chart follows conventional expectations, producing a straight line, the values on the vertical axis of the Base 2 Logarithmic chart show the principle of doubling congruences, meaning that each vertical unit represents a power of 2 (the vertical distance between 1 and 2 is the same as the distance between 2 and 4, and so on) while the horizontal distances remain linear, producing a curved line.
Base 10 Linear 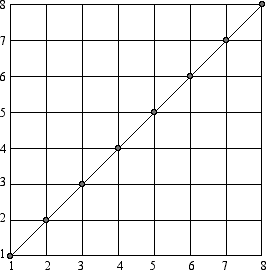 |
Base 2 Logarithmic 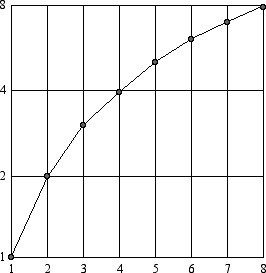 |
Both the linear scale and the logarithmic scale appear in this text. The logarithmic scale is accompanied by audio to show how we hear tonal relationships. Each logarithmic scale is followed by the same values shown on the linear scale, which is the same as a conventional number line. To be consistent in the way we express tones with numbers, we express the boundary tones as fractions or ratios as shown above; 1/1 and 2/1 are both labeled as tonic. The figure we are using to represent the source tonic should also reflect this representation.
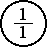
The process of placing a given value between 1 and 2 may be called justification. To justify a tone, we find the congruent tone which falls within the boundaries by multiplying or dividing by 2 any number of times. Multplying by 2 will result in a congruent tone which sounds higher in pitch, while dividing by 2 results in a congruent tone sounding lower in pitch.
Having established these boundaries, we have only one tone, which is relatively uninteresting. The system needs more tones; how will we generate them?
NEXT: 3 Tones