
In this chapter, linear interval measurement is explained. NOTE: Some elementary arithmetic is used in this section.
The number line we have been using can be seen as a kind of ruler for measuring tones and intervals. The boundaries of this number line are the first two harmonics, 1 and 2, which represent the octave.

When values are measured using this ruler, we get nonintuitive results, as demonstrated by the value 1.5 = 3/2.

1.5 is supposed to be a midpoint between 1 and 2, but here it is shown slightly to the right of center, because this is the way we hear this value as a pitch. Recall that our musical measurements produce a curved line where we would normally expect a straight one.
Normal 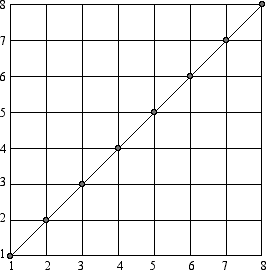 |
Musical 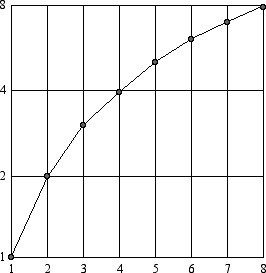 |
The musical ruler differs from a normal ruler in two important ways:
In short, this ruler does not work the way we would normally expect a ruler to work. We would rather have a ruler starting with zero where the midpoint falls in the middle.
We can build a tone ruler starting at zero fairly easily. Recalling that the number 2 represents the octave, we can apply to the following numerical fact for musical purposes.
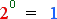
To clarify the usefulness of this statement, we replace the number 1 with the ratio 1/1.
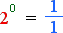
For our purpose, this statement has the following meaning.
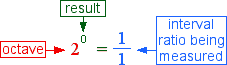
Which looks this way using rulers.

The top number line looks like a normal ruler; the tone 1/1 measured against the octave results in a distace of zero, as would be expected. A second numerical statement supplies a maximum value the other end of the ruler.
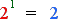
To clarify our purpose, we express the number 2 with the ratio 2/1.
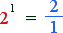
This statement has the following meaning for our purpose.
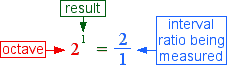
Which appears this way on a tone ruler.

When the tone 2/1 is measured against the octave, a distace of 1 results. We have laid the foundation for a tone ruler which measures distances within an octave, giving results between zero and 1.
The result expressed in our two numerical statements seems to be in the wrong place. We would expect a result to be on the right, after the equals sign.
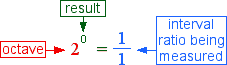
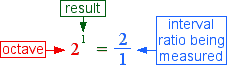
The result can be placed correctly by using the expression log, short for logarithm (meaning ratio number after Greek). Using logs, elements can be rearranged so that the result is on the right.
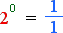
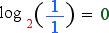
The meaning ot the elements remains the same.
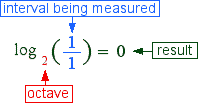
A measure of zero still results for the lower tonic.

The distance from the lower to the upper tonic still measures 1.
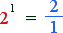
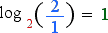


We now have a tone ruler with a single unit for measuring distances within an octave, properly expressed as an equation with the result on the right.
Our tone ruler represents one large unit, not unlike the foot of a foot ruler. But unlike a foot ruler, we have no smaller units. Smaller units would of course be useful for more precise measuring. How can this be done? We simply multiply the left side of the equation by the number of desired divisions, shown here as n.

While zero results for the measure of 1/1 regardless of the number of units on the ruler, the measure of the octave 2/1 is equal to the total number of desired units n.


How many units should our tone ruler have? One useful answer to this question is given in the next section.
NEXT: Cents